Problema nº 8 de variación de la dilatación volumétrica de sólidos y líquidos - TP01

Enunciado del ejercicio nº 8

Un frasco de vidrio (α = 0,00000861) esta lleno de mercurio a 0 °C. Se calienta hasta 100 °C y se derraman 1,5 cm³ a esa temperatura. ¿Cuál es el volumen del frasco?

Desarrollo

Datos:

t₁ = 0 °C

t₂ = 100 °C

V = 1,5 cm³ (volumen excedente de mercurio)

α = 0,00000861/°C (coeficiente de dilatación lineal del hierro)

γ = 0,000182/°C (coeficiente de dilatación volumétrica de del mercurio)

Fórmulas:

ΔV_c = 3·α·V_1c·Δt° (dilatación volumétrica del frasco de vidrio)

ΔVₘ = γ·V₁ₘ·Δt° (dilatación volumétrica del mercurio)

Solución

Se asume que con 0 °C el volumen de mercurio se encuentra enrasado con el borde del frasco de vidrio, es decir el mismo volumen inicial para ambos:

V₁ₘ = V_1c = V₁

Y:

V₂ₘ - V_2c = 1,5 cm³ (1)

Entonces:

ΔVₘ = γ·V₁ₘ·Δt°
V₂ₘ - V₁ₘ = γ·V₁ₘ·Δt°
V₂ₘ - V₁ = γ·V₁·Δt°

ΔV_c = 3·α·V_1c·Δt°
V_2c - V_1c = 3·α·V_1c·Δt°
V_2c - V₁ = 3·α·V₁·Δt°

Despejamos V₁ en ambas ecuaciones:

V₂ₘ - V₁ = γ·V₁·Δt°
V₂ₘ = γ·V₁·Δt° + V₁
V₂ₘ = (γ·Δt° + 1)·V₁
V₂ₘ/(γ·Δt° + 1) = V₁ (3)

V_2c - V₁ = 3·α·V₁·Δt°
V_2c = 3·α·V₁·Δt° + V₁
V_2c = (3·α·Δt° + 1)·V₁
V_2c/(3·α·Δt° + 1) = V₁ (4)

Igualamos las ecuaciones (3) y (4):

V₂ₘ·(3·α·Δt° + 1) = V_2c·(γ·Δt° + 1) (2)

De la ecuación (1) despejamos V₂ₘ:

V₂ₘ = V_2c + 1,5 cm³

Reemplazamos V₂ₘ en la ecuación (2):

(V_2c + 1,5 cm³)·(3·α·Δt° + 1) = V_2c·(γ·Δt° + 1) (2)

A continuación despejamos V_2c:

V_2c·(3·α·Δt° + 1) + 1,5 cm³·(3·α·Δt° + 1) = V_2c·(γ·Δt° + 1)

V_2c·(3·α·Δt° + 1) - V_2c·(γ·Δt° + 1) = -1,5 cm³·(3·α·Δt° + 1)

V_2c·[(3·α·Δt° + 1) - (γ·Δt° + 1)] = -1,5 cm³·(3·α·Δt° + 1)

V_2c·(3·α·Δt° + 1 - γ·Δt° + 1) = -1,5 cm³·(3·α·Δt° + 1)

V_2c·(3·α·Δt° - γ·Δt°) = -1,5 cm³·(3·α·Δt° + 1)

V_2c·(3·α - γ)·Δt° = -1,5 cm³·(3·α·Δt° + 1)

Reemplazamos por los valores y calculamos:

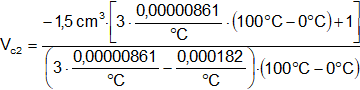
Se recomienda seguir atentamente la simplificación de las unidades y los signos.

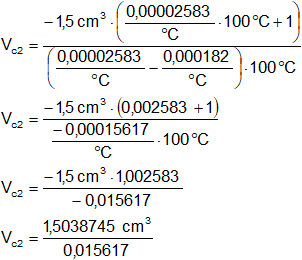
V_2c = 96,2972722 cm³

Hallamos el volumen final del frasco de vidrio. Ahora calcularemos el volumen inicial del frasco de vidrio con la ecuación (3):

Reemplazamos por los valores y calculamos:

V₁ = 96,04917718 cm³

Resultado, el volumen del frasco de vidrio es:

V₁ = 96 cm³

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP01
• | Siguiente ›

Ejemplo, ¿cuánto aumenta el volumen del mercurio al calentarlo dentro de un recipiente de vidrio?