Problema n° 5 de trabajo y potencia, energía cinética en un plano inclinado - TP02

Enunciado del ejercicio n° 5

Un cuerpo de 200 N se desliza por un plano inclinado de 15 m de largo y 3,5 de alto, calcular:

a) ¿Qué aceleración adquiere?

b) ¿Qué energía cinética tendrá a los 3 s?

c) ¿Qué espacio recorrió en ese tiempo?

Desarrollo

Datos:

P = 200 N

l = 15 m

h = 3,5 m

t = 3 s

Fórmulas:

P = m·g

v_f - vᵢ = a·t

Δx = vᵢ·t + ½·a·t²

E_c = ½·m·v²

Esquema:

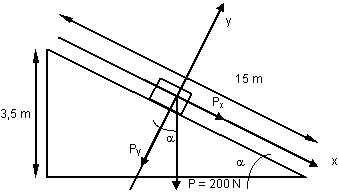
Esquema del cuerpo y la fuerza en un plano inclinado

Solución

a)

En el eje X:

∑Fₓ = m·a

Pₓ = m·a

Pero:

Pₓ = P·sen α

m·a = P·sen α

m·a = m·g·sen α

a = g·sen α

Por otra parte:

a = 9,807 (m/s²)·0,233

Resultado, la aceleración del cuerpo es:

a = 2,29 m/s²

b)

Suponiendo que parte del reposo:

v_f = a·t

Luego:

E_c = ½·m·v_f²

E_c = ½·m·(a·t)²

Resultado, la energía cinética del cuerpo a los 3 s es:

E_c = 480,54 J

c)

e = ½·a·t²

e = ½·2,29 m/s²·(3 s)²

Resultado, el espacio recorrió por el cuerpo en 3 s es:

e = 10,29 m

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP02
• | Siguiente ›

Ejemplo, cómo calcular la energía cinética en un plano inclinado