Problema nº 1 de energía y potencia, trabajo realizado por una fuerza - TP04
Enunciado del ejercicio nº 1
Un carrito de 5 N es desplazado 3 m a lo largo de un plano horizontal mediante una fuerza de 22 N. Luego esa fuerza se transforma en otra de 35 N a través de 2 m. Determinar:
a) El trabajo efectuado sobre el carrito.
b) La energía cinética total.
c) La velocidad que alcanzó el carrito.
Desarrollo
Datos:
P = 5 N
F₁ = 22 N
F₂ = 35 N
d₁ = 3 m
d₂ = 2 m
Fórmulas:
P = m·g
F = m·a
LFC = ΔEₘ
ΔEc = ½·m·v²
g = 9,8 m/s²
Esquema:
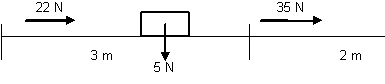
Esquema de los cuerpos y las fuerzas
Solución
a)
El teorema de la energía mecánica dice que el trabajo de las fuerzas conservativas es igual a la variación de la energía mecánica del sistema.
LFC = ΔEₘ
Desarrollamos esta ecuación:
LFC = ΔEₘ = ΔEc + ΔEₚ
Como el movimiento es horizontal la variación de la energía potencial es nula.
LFC = ΔEₘ = ΔEc
La variación de la energía cinética total de este sistema es:
ΔEcT = ΔEc1 + ΔEc2
ΔEcT = ½·m·vf1² - ½·m·vᵢ₁² + ½·m·vf2² - ½·m·vᵢ₁²
ΔEcT = ½·m·(vf1² - vᵢ₁² + vf2² vᵢ₁²)
No hay rozamiento y:
vᵢ₁ = 0
vf1 = vᵢ₂
Por lo tanto:
ΔEcT = ½·m·vf2²
Adaptándolo a la ecuación de trabajo:
LFC = ½·m·vf2²
Como no hay fuerzas "no conservativas" el trabajo del sistema es igual a la variación de la energía cinética del sistema (o total). El trabajo y la variación de la energía cinética tienen el mismo valor pero distinto sentido.
Mediante cinemática calculamos la velocidad final pero por partes, hay que obtener la masa del cuerpo y la aceleración en cada tramo:
Se emplea g = 9,8 m/s²
La masa del cuerpo es:
P = m·g
![]()
Despejamos la masa m:
![]()
m = 0,51 kg
La aceleración en el primer tramo la obtenemos de:
F₁ = m·a₁
![]()
Reemplazamos por los valores y calculamos:
![]()
a₁ = 43,16 m/s²
vf1² - vᵢ₁² = 2·a₁·e₁
Sabemos que: vᵢ₁ = 0
vf1² = 2·a₁·e₁
![]()
Reemplazamos por los valores y calculamos:
![]()
vf1 = 16,09 m/s
Para el segundo tramo
F₂ = m·a₂
![]()
Reemplazamos por los valores y calculamos:
![]()
a₂ = 68,67 m/s²
vf2² - vᵢ₂² = 2·a₂·e₂
Pero vᵢ₂² = vf1²:
vf2² - vf1² = 2·a₂·e₂
vf2² = 2·a₂·e₂ + vf1²
![]()
Reemplazamos por los valores y calculamos:
![]()
vf2 = 23,1 m/s
Resultado, la velocidad que alcanzó el carrito es:
vf2 = 23,1 m/s
Con este último dato calculamos el trabajo del sistema:
LFC = ½·m·vf2²
LFC = ½·0,51 kg·(23,10 m/s)²
Resultado, el trabajo efectuado por las fuerzas sobre el carrito es:
LFC = 136 J
Por supuesto el trabajo se puede calcular sencillamente por:
LT = L₁ + L₂
LT = 22 N·3 m + 35 N·2 m
LT = 136 J
Pero no tiene sentido hacerlo fácil!
b)
Luego la energía cinética:
ΔEcT = ½·m·vf2²
LFC = ½·0,51 kg·(23,10 m/s)²
Resultado, la energía cinética total es:
LFC = 136 J
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP04
- | Siguiente ›
Ejemplo, cómo calcular el trabajo realizado por una fuerza