Problema nº 9 de trabajo, energía y potencia, fuerza resultante - TP05
Enunciado del ejercicio nº 9
El conductor de un coche de 1.200 kg nota que el coche disminuye su velocidad desde 20 m/s a 15 m/s en una distancia de 120 m sobre suelo nivelado.
¿De qué magnitud es la fuerza que se opone al movimiento?
Desarrollo
Datos:
vᵢ = 20 m/s
vf = 15 m/s
d = 120 m
m = 1.200 kg
Fórmulas:
ΔEM = ΔEC + ΔEP + LFr
Esquema:
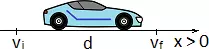
Solución
La energía potencial es nula porque no hay cambio de altura.
ΔEM = ΔEC + 0 + LFr
No habla de trabajo, por lo tanto:
ΔEM = ΔEC + 0 + 0
Entonces:
ΔEM = ΔEC
ΔEM = ECf - ECi
La variación de la energía mecánica es el trabajo que realiza la fuerza resultante del sistema:
ΔEM = LFT
Igualando:
LFT = ECf - ECi
Desglosamos los términos:
FT·d = ½·m·vf² - ½·m·vᵢ²
FT = (½·m·vf² - ½·m·vᵢ²)/d
FT = [½·1.200 kg·(20 m/s)² - ½·1.200 kg·(15 m/s)²]/120 m
FT = (240.000 kg·m²/s² - 135.000 kg·m²/s²)/120 m
FT = (105.000 kg·m²/s²)/120 m
FT = 875 kg·m/s²
Respuesta, FT = 875 N.
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP05
- | Siguiente ›
Ejemplo, cómo calcular la fuerza resultante