Problema nº 7 de trabajo y potencia, fuerza motriz - TP06

Enunciado del ejercicio nº 7

Un móvil de 3.200 kgf sube por un plano inclinado que asciende 5 m cada 100 m medidos sobre el plano. Calcular la fuerza motriz sabiendo que:

a) Se mantiene constante.

b) En 200 m pasa de 40 a 60 km/h.

c) En el mismo camino disminuye de 40 a 20 km/h.

Desarrollo

Datos:

P = 3.200 kgf

h = 5 m

d = 100 m

g = 9,81 m/s²

Fórmulas:

P = m·g

ΔE_M = ΔE_c + ΔEₚ

Esquema:

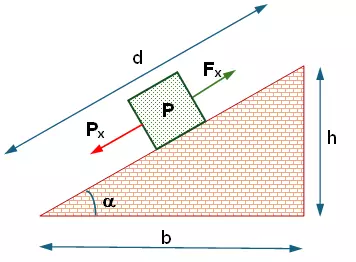
Esquema del cuerpo y el peso en un plano inclinado

Solución

a)

La fuerza motriz es la fuerza mínima necesaria para mover el bloque hacia arriba con velocidad constante.

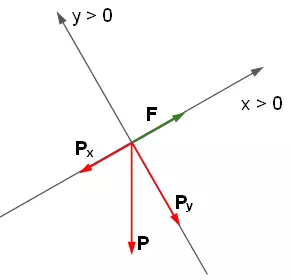
Fₓ = Pₓ

La componente del peso en x es:

Fₓ = P·sen α

Reemplazamos:

Reemplazamos por los valores y calculamos:

Fₓ = 3.200 kgf·0,05

Resultado a), la fuerza motriz es:

Fₓ = 160 kgf

b)

Según la variación de la energía mecánica:

ΔE_M = ΔE_c + ΔEₚ

Y:

L = ΔE_M = ΔE_c + ΔEₚ

Por tanto:

L = ΔE_c + ΔEₚ

Luego:

L = Fₓ·d = ΔE_c + ΔEₚ

Fₓ·d = ΔE_c + ΔEₚ

Continuamos:

Fₓ·d = E_c2 - E_c1 + Eₚ₂ - Eₚ₁

Si hₚ₁ = 0, entonces:

Fₓ·d = E_c2 - E_c1 + Eₚ₂

Calculamos E_c2, E_c1 y Eₚ₂:

E_c2 = ½·m·v_c2²

E_c1 = ½·m·v_c1²

Eₚ₂ = m·g·hₚ₂

Por tanto:

m = 326,197757 kg = 326,2 kg

Convertimos las unidades de velocidad:

v₁ = 11,11 m/s

v₂ = 16,67 m/s

Reemplazamos por los datos y calculamos:

E_c2 = ½·326,2 kg·(16,67 m/s)²

E_c2 = 163,1 kg·277,77 m²/s²

E_c2 = 45.303,97 kgf·m

E_c1 = ½·326,2 kg·(11,11 m/s)²

E_c1 = 163,1 kg·123,457 m²/s²

E_c1 = 20.135,69 kgf·m

Eₚ₂ = 326,2 kg·9,81 m/s²·10 m

Eₚ₂ = 32.000 kgf·m

Luego:

Fₓ·d = E_c2 - E_c1 + Eₚ₂

Fₓ·d = 45.303,97 kgf·m - 20.135,69 kgf·m + 32.000 kgf·m

Fₓ·d = 57.168,28 kgf·m

Fₓ = 285,8414 kgf

Resultado b), la fuerza motriz de 40 a 60 km/h es:

Fₓ = 285,85 kgf

c)

Procedemos como en el caso anterior.

Según la variación de la energía mecánica:

ΔE_M = ΔE_c + ΔEₚ

Y:

L = ΔE_M = ΔE_c + ΔEₚ

Por tanto:

L = ΔE_c + ΔEₚ

Luego:

L = Fₓ·d = ΔE_c + ΔEₚ

Fₓ·d = ΔE_c + ΔEₚ

Continuamos:

Fₓ·d = E_c2 - E_c1 + Eₚ₂ - Eₚ₁

Si hₚ₁ = 0, entonces:

Fₓ·d = E_c2 - E_c1 + Eₚ₂

Calculamos E_c2, E_c1 y Eₚ₂:

E_c2 = ½·m·v_c2²

E_c1 = ½·m·v_c1²

Eₚ₂ = m·g·hₚ₂

Por tanto:

m = 326,197757 kg = 326,2 kg

E_c2 = ½·326,2 kg·(5,55 m/s)²

E_c2 = 163,1 kg·30,864 m²/s²

E_c2 = 5.033,9184 kgf·m

E_c1 = ½·326,2 kg·(11,11 m/s)²

E_c1 = 163,1 kg·123,457 m²/s²

E_c1 = 20.135,69 kgf·m

Eₚ₂ = 326,2 kg·9,81 m/s²·10 m

Eₚ₂ = 32.000 kgf·m

Luego:

Fₓ·d = E_c2 - E_c1 + Eₚ₂

Fₓ·d = 5.033,92 kgf·m - 20.135,69 kgf·m + 32.000 kgf·m

Fₓ·d = 16.898,2284 kgf·m

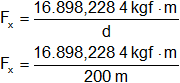
Fₓ = 84,4911 kgf

Resultado c), la fuerza motriz de 40 a 20 km/h es:

Fₓ = 84,49 kgf

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP06
• | Siguiente ›

Ejemplo, cómo calcular la fuerza motriz