Problema nº 8 de energía, trabajo realizado por la fuerza ascencional - TP07
Enunciado del ejercicio nº 8
La fuerza ascensional de un globo es la diferencia entre el empuje y su peso. El empuje es el peso del aire desalojado por el globo. Calcular el trabajo de la fuerza ascensional en elevar un globo de 120 kgf y 4 metros de radio a una altura de 60 metros. La densidad del aire es δ = 1,293 kg/m³.
Desarrollo
Datos:
P = 120 kgf
h = 60 m
r = 4 m
δ = 1,293 kg/m³
g = 9,80665 m/s²
Fórmulas:
E = δ·g·Vd (Principio de Arquímedes - Empuje)
Fa = E - P
Solución
Para calcular el empuje E necesitamos determinar el volumen del globo, lo consideramos una esfera:
| Vd = | 4 | ·π·r³ |
| 3 |
Reemplazamos por los valores y calculamos:
| Vd = | 4 | ·3,14159·(4 m)³ |
| 3 |
| Vd = | 4 | ·3,14159·64 m³ |
| 3 |
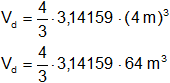
Vd = 268,0825731 m³
Hallamos el empuje E:
E = δ·g·Vd
E = 1,293 kg/m³·9,80665 m/s²·268,0825731 m³
El empuje del globo es:
E = 3.399,286611 N
Adecuamos las unidades:
| P = 120 kgf· | 9,80665 N |
| 1 kgf |
P = 1.176,798 N
Aplicamos la fórmula de fuerza ascencional:
Fa = E - P
Reemplazamos por los valores y calculamos:
Fa = 3.399,286611 N - 1.176,798 N
Fa = 2.222,488611 N
Finalmente calculamos el trabajo de la fuerza ascencional:
L = Fa·h
L = 2.222,488611 N·60 m
L = 133.349,3167 J
Resultado, el trabajo de la fuerza ascencional es:
L = 133.349 J
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP07
- | Siguiente ›
Ejemplo, cómo calcular el trabajo de la fuerza ascencional