Problema nº 1 de trabajo y potencia, variación de la energía cinética - TP09
Enunciado del ejercicio nº 1
Sobre un vagón en reposo de 1.600 kg actúa una fuerza de 20 N durante 3 minutos. Calcular el aumento de la energía cinética del vagón.
Desarrollo
Datos:
m = 1.600 kg
F = 20 N
t = 3 min
Fórmulas:
ΔEc = Ec2 - Ec1
Ec = ½·m·v²
Solución
Aplicamos la ecuación de la variación de la energía cinética para ambos instantes:
ΔEc = Ec2 - Ec1
ΔEc = ½·m·v₂² - ½·m·v₁²
v₁ = 0
ΔEc = ½·m·v₂² (1)
Para obtener el valor de v₂ debemos recurrir a la ecuación horaria de la velocidad (cinemática):
v₂ = v₁ + a·t
v₁ = 0
v₂ = a·t (2)
Falta el dato de la aceleración, la obtenemos de la fuerza:
F = m·a
Despejamos a:
| a = | F |
| m |
Reemplazamos en (2):
| v₂ = | F·t |
| m |
Reemplazamos en (1):
| ΔEc = ½·m·( | F·t | )² |
| m |
Adecuamos las unidades:
| t = 3 min· | 60 s |
| 1 min |
t = 180 s
Reemplazamos por los valores y calculamos:
| ΔEc = ½·1.600 kg·( | 20 N·180 s | )² |
| 1.600 kg |
| ΔEc = 800 kg·( | 3.600 N·s | )² |
| 1.600 kg |
ΔEc = 800 kg·(2,25 N·s/kg)²
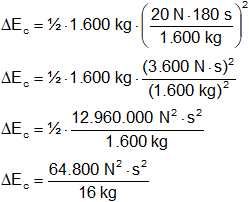
ΔEc = 4.050 N²·s²/kg
ΔEc = 4.050 N·N·s²/kg
ΔEc = 4.050 N·kg·m/s²·s²/kg
ΔEc = 4.050 N·m
Resultado, la variación de la energía cinética es:
ΔEc = 4.050 J
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP09
- | Siguiente ›
Ejemplo, cómo calcular la variación de la energía cinética