Problema nº 3 de energía cinética y masas - TP09
Enunciado del ejercicio nº 3
Dos masas m₁ y m₂ separadas por una altura de 12 metros, tienen la misma energía, aunque la que está más abajo (m₂) tiene 4 veces más velocidad que la otra (m₁).
Calcular las masas si suman mₜ = 22 kg y la masa m₁ situada más arriba, posee una energía cinética Ec1 = 4.000 J.
Desarrollo
Datos:
Δh = 12 m
mₜ = 22 kg
Ec1 = 4.000 J
g = 9,80665 m/s²
Fórmulas:
ΔEM = ΔEc + ΔEₚ
Ec = ½·m·v²
Esquema:
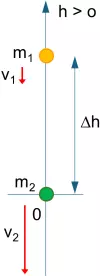
Solución
Aplicamos la ecuación de la energía mecánica a ambas masas:
ΔEM1 = ΔEc1 + ΔEₚ₁
ΔEM2 = ΔEc2 + ΔEₚ₂
La energía total es la misma, por tanto:
ΔEM1 = ΔEM2
ΔEc1 + ΔEₚ₁ = ΔEc2 + ΔEₚ₂
Como se trata de la energía puntual descartamos la variación:
Ec1 + Eₚ₁ = Ec2 + Eₚ₂
½·m₁·v₁² + m₁·g·h₁ = ½·m₂·v₂² + m₂·g·h₂ (1)
El enunciado condiciona a:
v₂ = 4·v₁ (2)
mₜ = m₁ + m₂ (3)
Reemplazamos (2) en (1):
½·m₁·v₁² + m₁·g·h₁ = ½·m₂·(4·v₁)² + m₂·g·h₂
Elegimos el origen de las ordenadas (altura) en h₂, por lo que:
h₂ = 0
Δh = h₁ - h₂
12 m = h₁ - h₁
12 m = h₁ (4)
Entonces:
½·m₁·v₁² + m₁·g·h₁ = ½·m₂·16·v₁²
½·m₁·v₁² + m₁·g·h₁ = 8·m₂·v₁² (5)
Luego, despejamos la velocidad v₁ de la ecuación de energía cinética:
Ec1 = ½·m₁·v₁²
| v₁² = | 2·Ec1 |
| m₁ |
Reemplazamos en (5):
| ½·m₁· | 2·Ec1 | + m₁·g·h₁ = 8·m₂· | 2·Ec1 |
| m₁ | m₁ |
| Ec1 + m₁·g·h₁ = 16·m₂· | Ec1 |
| m₁ |
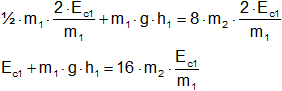
Por condición del enunciado (3):
mₜ - m₁ = m₂
| Ec1 + m₁·g·h₁ = 16·(mₜ - m₁)· | Ec1 |
| m₁ |
| Ec1 + m₁·g·h₁ = 16·mₜ· | Ec1 | - 16·m₁· | Ec1 |
| m₁ | m₁ |
| Ec1 + m₁·g·h₁ = 16·Ec1· | mₜ | - 16·Ec1· | m₁ |
| m₁ | m₁ |
| Ec1 + m₁·g·h₁ = 16·Ec1· | mₜ - m₁ |
| m₁ |
| Ec1 + m₁·g·h₁ - 16·Ec1· | mₜ - m₁ | = 0 |
| m₁ |
| Ec1·m₁ + m₁²·g·h₁ - 16·Ec1·(mₜ - m₁) | = 0 |
| m₁ |
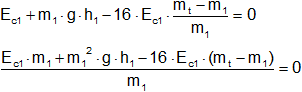
Ec1·m₁ + m₁²·g·h₁ - 16·Ec1·(mₜ - m₁) = 0
Ec1·m₁ + m₁²·g·h₁ - 16·Ec1·mₜ + 16·Ec1·m₁ = 0
m₁²·g·h₁ + 17·Ec1·m₁ - 16·Ec1·mₜ = 0
Reemplazamos por los valores:
m₁²·(9,80665 m/s²)·(12 m) + 17·(4.000 J)·m₁ - 16·(4.000 J)·(22 kg) = 0
117,6798 m²/s²·m₁² + 68.000 J·m₁ - 1.408.000 J·kg = 0
Aplicamos la ecuación de Báscara o Bhaskara:
| x1,2 = | -b ± √b² - 4·a·c |
| 2·a |
Siendo:
a = 117,6798 m²/s²
b = 68.000 J
c = -1.408.000 J·kg
| m₁(x,y) = | -68.000 J ± √(68.000 J)² - 4·117,6798 m²/s²·(-1.408.000 J·kg) |
| 2·117,6798 m²/s² |
| m₁(x,y) = | -68.000 J ± √4.624.000.000 J² + 662.772.633,6 m²/s²·J·kg |
| 235,3596 m²/s² |
| m₁(x,y) = | -68.000 J ± √4.624.000.000 J² + 662.772.633,6 J·J |
| 235,3596 m²/s² |
| m₁(x,y) = | -68.000 J ± √5.286.772.634 J² |
| 235,3596 m²/s² |
| m₁(x,y) = | -68.000 J ± 72.710,19621 J |
| 235,3596 m²/s² |
Obtendremos dos valores para m₁:
| m₁x = | -68.000 J + 72.710,19621 J |
| 235,3596 m²/s² |
| m₁x = | 4.710,196215 J |
| 235,3596 m²/s² |
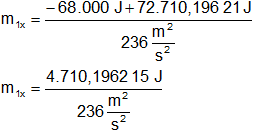
m₁x = 20,01276436 kg
| m₁y = | -68.000 J - 72.710,19621 J |
| 235,3596 m²/s² |
| m₁y = | -140.710,1962 J |
| 235,3596 m²/s² |
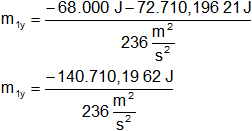
m₁y = -597,8519517 kg (se descarta, no existe la masa negativa)
m₁ = 20 kg
Reemplazamos en (3):
mₜ - m₁ = m₂
22 kg - 20 kg = m₂
m₂ = 2 kg
Resultado, los valores de las masas son:
m₁ = 20 kg; m₂ = 2 kg
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP09
- | Siguiente ›
Ejemplo, cómo calcular la variación de la energía cinética