Problema nº 6 de potencia y energía, altura máxima - TP09

Enunciado del ejercicio nº 6

Un automóvil de 200 HP y 1.500 kg, parte del reposo y a los 20 metros se encuentra con una pendiente. Calcular a qué altura llega si al entrar en la pendiente se apaga el motor.

Desarrollo

Datos:

W = 200 HP

m = 1.500 kg

v₁ = 0 m/s

d = 20 m

g = 9,80665 m/s²

Fórmulas:

v₂² = v₁² + 2·a·Δx

x₂ = x₁ + v₁·t + ½·a·t²

ΔE_M = ΔE_c + ΔEₚ

E_c = ½·m·v²

Solución

El movimiento se divide en dos etapas, la primera inicia la marcha hasta alcanzar la velocidad v₂ conque iniciará el ascenso a la pendiente, la segunda etapa es la subida por la pendiente.

Para el primer tramo del recorrido aplicamos, de cinemática, la ecuación combinada para hallar la aceleración:

v₂² = v₁² + 2·a·Δx

v₁ = 0 m/s

v₂² = 2·a·Δx

Δx = x₂ - x₁

h₁ = 0

Δx = x₂ = d

v₂² = 2·a·d (1)

Luego, aplicamos de cinemática la ecuación horaria de posición:

x₂ = x₁ + v₁·t + ½·a·t²

Ya vimos que:

v₁ = 0 m/s; h₁ = 0 y x₂ = d

d = ½·a·t²

Despejamos t:

(2)

Donde t es el tiempo que demora en recorrer los 20 metros.

La velocidad v₂ es la velocidad luego de recorrer los 20 metros y a su vez es la velocidad inicial al llegar a la pendiente.

Para alcanzar dicha velocidad, el automóvil posee una potencia de 200 HP, que se expresa:

Desarrollamos esta expresión:

Despejamos t:

Reemplazamos en (2):

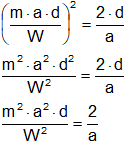
W² = ½·m²·a³·d (3)

Despejamos a de (1):

v₂² = 2·a·d

Reemplazamos en (3):

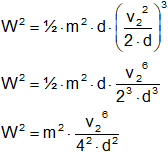
Aplicamos raíz cuadrada en ambos términos:

De donde:

(4)

Para la segunda etapa aplicamos la ecuación de la energía mecánica:

ΔE_M = ΔE_c + ΔEₚ

Las fuerzas son conservativas:

0 = ΔE_c + ΔEₚ

ΔE_c = ΔEₚ

Al detenerse el motor toda la energía cinética se transformará en energía potencial hasta que se detenga el automóvil en la altura máxima h₃:

Eₚ₃ = E_c2

m·g·h₃ = ½·m·v₂²

Cancelamos las masas:

g·h₃ = ½·v₂²

Despejamos h₃:

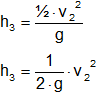
Reemplazamos v₂ de la (4):

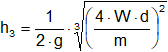
Convertimos las unidades:

W = 149.140 W

Reemplazamos por los valores y calculamos:

h₃ = 20,31629794 m

Resultado, la altura máxima es:

h₃ = 20,32 m

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP09
• | Siguiente ›

Ejemplo, cómo calcular la altura máxima