Problema nº 8 de potencia y energía, altura máxima - TP09

Enunciado del ejercicio nº 8

Un cuerpo es arrojado verticalmente hacia arriba con una velocidad inicial de 4 m/s. Calcular la altura máxima que alcanza. Compara la expresión de la altura máxima con la correspondiente a lanzamiento vertical de cinemática.

Desarrollo

Datos:

v₁ = 4 m/s

g = 9,80665 m/s²

Fórmulas:

ΔE_M = ΔE_c + ΔEₚ

E_c = ½·m·v²

Eₚ = m·g·h

Solución

Aplicamos la ecuación de la energía mecánica:

ΔE_M = ΔE_c + ΔEₚ

Las fuerzas son conservativas:

ΔE_M = ΔE_c + ΔEₚ = 0

ΔE_c + ΔEₚ = 0

En el lanzamiento vertical hacia arriba hasta alcanzar la altura máxima, toda la energía cinética se transforma en energía potencial.

E_c1 + Eₚ₁ = E_c2 + Eₚ₂

½·m·v₁² + m·g·h₁ = ½·m·v₂² + m·g·h₂

Elegimos el origen de las ordenadas (altura) en h₁, por lo que:

h₁ = 0

h₂: altura máxima

½·m·v₁² = ½·m·v₂² + m·g·h₂

Cuando alcanza la altura máxima:

v₂ = 0

½·m·v₁² = m·g·h₂

Cancelamos la masa m:

½·v₁² = g·h₂

v₁² = 2·g·h₂

Esta expresión es la misma que la ecuación combinada de cinemática.

Despejamos h₂:

Reemplazamos por los valores y calculamos:

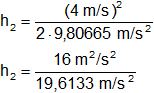
h₂ = 0,81577297 m

Resultado, la altura máxima que alcanza es:

h₂ = 0,82 m

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP09
• | Siguiente ›

Ejemplo, cómo calcular la altura máxima