Derivada primera: Recta tangente a una curva en un punto

El valor numérico de la derivada de una función en un punto perteneciente a dicha función da como resultado el valor de la pendiente de la recta tangente a la función en ese punto.

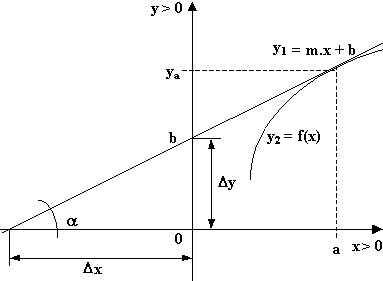
Gráfica de la curva, la recta tangente a la curva y su pendiente

m = Δy/Δx ⇒ m = tg α

y₂' = f'(x)

Pero y₂' en a:

tg α = f'(a) ⇒ m = f'(a)

Por lo tanto la ecuación de la recta tangente a la curva en el punto a, es:

y₁ = f'(a)·x + b

Las coordenadas forman el punto de intersección entre la recta (tangente a la curva) y la curva.

Casos de aplicación:

1) Dado el punto P(a; yₐ), hallar la ecuación de la recta tangente

a) Derivar la función de la curva.
y₂' = f'(x)

b) Reemplazar en la derivada x por el valor a.
y₂' = f'(a)

c) El resultado es la pendiente m.
m = f'(a)

d) Armar la ecuación de la recta con m y el punto dado.
y₁ = m·(x - a) + yₐ

2) Dadas las ecuaciones de la recta y la curva, verificar que la recta sea tangente a la curva

a) Se debe hallar el punto de intersección entre ambas funciones, esto se logra igualando las funciones.
y₁ = y₂ ⇒ m·x + b = f(x)

b) Despejando x se obtiene el valor de a, ya que x = a

c) Con el valor de x reemplazar en y₁ ó y₂ para hallar yₐ

d) El punto de intersección será:
P(a; yₐ)

e) Derivar la función de la curva.
y₂' = f'(x)

f) Reemplazar en la derivada x por el valor a.
y₂' = f'(a)

g) Verificar que f'(a) sea igual a m.
y₂' = m

3) Dada una recta cualquiera (y = m₃·x + b₃), hallar la recta tangente paralela a una curva

a) La pendiente de esta recta (m₃) debe ser igual a la pendiente de la recta tangente (m₁).
m₃ = m₁

b) Además, esta pendiente, debe ser igual al valor de la derivada en el punto de intersección.
m₃ = f'(a) ⇒ m₃ = f'(x)

c) Despejar el x = a

d) Con el valor de x reemplazar en y₂ para hallar yₐ

e) El punto de intersección será:
P(a; yₐ)

f) Armar la ecuación de la recta tangente con m₃ y el punto hallado.
y₁ = m₃·(x - a) + yₐ

Autor: Ricardo Santiago Netto. Argentina

¿Qué representa la pendiente de una curva? ¿Qué es la recta tangente a una curva en un punto?