Derivada de una función (Quinta parte)
Regla de la cadena
Derivada de la función xm/n
Sea f(x) = xm/n
Se eleva a n, f(x)ⁿ = xᵐ
Se deriva:
n·f(x)⁽ⁿ ⁻ ¹⁾·f'(x) = m·xᵐ ⁻ ¹
Pero f(x)⁽ⁿ ⁻ ¹⁾ = (xm/n)⁽ⁿ ⁻ ¹⁾
Despejando f(x),
| f'(x) = | m·xᵐ ⁻ ¹ | = | m | ·x(m/n) - 1 |
| n·(xm/n)⁽ⁿ ⁻ ¹⁾ | n |
Regla de la cadena para las funciones u1/n y um/n
Si en las dos funciones anteriores se tiene una función dependiente de la variable x, u(x), en lugar de la función x, se obtienen las siguientes derivadas:
Si f(x) = u1/n ⇒ f'(x) = (u1/n)'
| f'(x) = | u' |
| n·u(n - 1)/n |
En particular:
| (√u)' = | u' |
| 2·√u |
Si g(x) = um/n ⇒ g'(x) = (um/n)'
| g'(x) = | m | ·u(m/n) - 1·u' |
| n |
Para obtener estas igualdades, basta aplicar la regla de la cadena.
Ejemplos de cálculo de derivadas aplicando la regla de la cadena para funciones u1/n y um/n
Ejemplo nº 1
¿Cuál es la función derivada de f(x) = √x² + sen x
Solución
- Se escribe la raíz en forma de potencia: √x² + sen x = (x² + sen x)½
- Se trata de calcular una derivada de la forma u½
Si u = x² + sen x, u' = 2·x + cos x
Ejemplo nº 2
Obsérvese que en este caso n = 2
∛[(x + 1)/x]² = [(x + 1)/x]⅔
u = (x + 1)/x
u' = [1·x - (x + 1)·1]/x²
u' = (x - x - 1)/x²
u' = -1/x²
Solución
1) Se escribe la raíz en forma de potencia:
f'(x) = [√x² + sen x]'
f'(x) = (√u)'
f'(x) = u'/(2·√u)
f'(x) = (2·x + cos x)/(2·√x² + sen x
2) Calcular la derivada de f(x) = ∛[(x + 1)/x]²
Se aplica la fórmula:
| (um/n) = | m | ·um/n - 1·u' |
| n |
f'(x) = [∛[(x + 1)/x]²]'
f'(x) = ⅔·[(x + 1)/x](⅔ - 1)·(-1/x²)
f'(x) = (-⅔·x²)·[(x + 1)/x]⁻⅓
f'(x) = (-⅔·x²)·[x/(x + 1)]⅓
f'(x) = (-⅔·x²)·∛x/(x + 1)
Funciones trigonométricas inversas
La función sen x definida en [-π/2, π/2] toma todos los valores del intervalo [-1, 1] una sola vez, es decir, dos números distintos de [-π/2, π/2] alcanzan valores distintos en [-1, 1].
Esto quiere decir que existe una aplicación biyectiva de [- π/2, π/2] a [-1, 1] mediante la función seno. En estas condiciones se puede definir la aplicación inversa de f(x) = sen x, llamada «arco-seno» y que se simboliza por arcsen x.
Así, arcsen ½ = π/6, pues sen π/6 = ½
arcsen -√3/2 = -π/3, pues sen -π/3 = -sen π/3 = -√3/2
| [- | π | , | π | ] | f ⟶ sen x | [-1, 1] | f⁻¹ ⟶ arcsen x | [- | π | , | π | ] |
| 2 | 2 | 2 | 2 |
x ⟶ f(x) = sen x ⟶ f⁻¹ [f(x)] = f⁻¹ (sen x) = arcsen (sen x) = x
Derivada de la función arcsen x
Si y = arcsen x = f⁻¹(x), aplicando f, f(y) = f(f⁻¹(x)) = x, es decir, sen y = x.
Derivando respecto a x, por la regla de la cadena, y'·cos y = 1 ó y' = 1/cos y
De la conocida fórmula sen² y + cos² y = 1, cos² y = 1 - sen² y ⇒ cos y = ±√1 - sen² y
Pero en el intervalo [-π/2, π/2] la función cos y es positiva, por lo que cos y = √1 - sen² y
Por último, y puesto que sen y = x, cos y = √1 - x²
Llevando este resultado a la expresión y', y' = 1/√1 - x²
Si h(x) = arcsen x ⇒ h'(x) = 1/√1 - x²
Derivada de la función arccos x
Análogamente, la función cos x tiene una función inversa llamada «arco-coseno» y se simboliza por arccos x.
De y = arccos x se deduce x = cos y. Derivando por la regla de la cadena,
1 = -y'·sen y ⇒ y' = -1/sen y
Como sen y = √1 - cos² y = √1 - x², y' = -1/√1 - x²
Si h(x) = arccos x ⇒ h'(x) = -1/√1 - x²
Derivada de la función arctg x
La inversa de la función tg x se llama «arco-tangente» y se simboliza por arctg x.
y = arctg x, x = tg y. Derivando por la regla de la cadena,
1 = y'·(1 + tg² y) = y'·(1 + x²). Despejando y', y' = 1/(1 + x²)
Si h(x) = arctg x ⇒ h'(x) = 1/(1 + x²)
Derivada de la función arccotg x
La inversa de la función cotg x se llama arco-cotangente y se simboliza por arccotg x.
Si y = arccotg x, x = cotg y. Derivando esta igualdad por la regla de la cadena,
1 = -y'·(1 + cotg² y) = -y'·(1 + x²). Despejando y', y' = -1/(1 + x²)
Si h(x) = arccotg x ⇒ h'(x) = -1/(1 + x²)
Derivada de la función arcsec x
Análogamente a los casos anteriores, sec x tiene una función inversa llamada «arco secante» y simbolizada por arcsec x.
y = arcsec x, x = sec y. Derivando por la regla de la cadena,
1 = y'·sec y·tg y = y'·x·tg y (1)
Por trigonometría se sabe que 1 + tg² y = 1/cos² y = sec² y = x², de donde
tg² y = x² - 1 ⇒ tg y = √x² - 1
Sustituyendo este valor en la igualdad (1), 1 = y'·x·√x² - 1, y despejando y',
y' = 1/x·√x² - 1
Si h(x) = arcsec x ⇒ h'(x) = 1/x·√x² - 1
Derivada de la función arccosec x
Siguiendo los mismos pasos que en el caso anterior,
y = arccosec x, x = cosec y
Derivando: 1 = -y'·cosec y·cotg y = -y'·x·cotg y (1)
Como
1 + cotg² y = 1/sen² y = cosec² y = x², cotg² y = √x² - 1
Llevando este resultado a la igualdad (1) y despejando y',
y' = -1/x·√x² - 1
Si h(x) = arccosec x ⇒ h'(x) = -1/x·√x² - 1
Regla de la cadena trigonométrica inversas
Si en cada una de las funciones anteriores se tuviese una función de x, u(x), en lugar de la función x, las derivadas de las nuevas funciones compuestas se convierten, por la regla de la cadena en:
| f(x) | f'(x) |
| arcsen u | u'÷(√1 - u²) |
| arccos u | - u'÷(√1 - u²) |
| arctg u | u'/(1 + u²) |
| arccotg u | -u'/(1 + u²) |
| arcsec u | u'÷(u·√u² - 1) |
| arccosec u | - u'÷(u·√u² - 1) |
Ejemplos de cálculo de derivadas aplicando la regla de la cadena para funciones trigonométricas inversas
Ejemplo nº 1
Calcular la derivada de y = arcsen [(x + 1)/(x - 1)]
Solución
Si u = [(x + 1)/(x - 1)], por la derivada del cociente,
u' = [1·(x - 1) - (x + 1)·1]/(x - 1)²
u' = -2/(x - 1)²
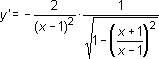
Ejemplo nº 2
Hallar la derivada de y = arctg (ln x)/x
Solución
Llamando
u = ln x/x
u' = [(1/x)·x - ln x·1]/x²
u' = (1 - ln x)/x²
y' = [(1 - ln x)/x²]·{1/[1 + (ln x/x)²]}
y' = [(1 - ln x)/x²]·{1/[1 + (ln x/x)²]}
y' = [(1 - ln x)/x²]·{x²/[x² + (ln x)²]}
y' = (1 - ln x)/[x² + (ln x)²]
Ejemplo nº 3
Calcular la derivada de y = arcsec (5·x³/3)
Solución
u = (5/3)·x³
u' = (5/3)·3·x²
u' = 5·x²
| y' = | 5·x² |
| (5/3)·x³·√(5·x³/3)² - 1 |
Ejemplo nº 4
¿Cuál es la derivada de y = arccosec √x² - 1
Solución
Si:
u = √x² - 1
u' = 2·x/(2·√x² - 1)
u' = x/√x² - 1
y' = -u'/(u·√u² - 1)
| - | x | -x | |||
| y' = | √x² - 1 | = | |||
| √x² - 1·√x² - 1 - 1 | (x² - 1)·√x² - 2 | ||||
Diferencial de una función
Sea una función y = f(x). Dado un punto de abscisa x, se le dota de un pequeñísimo incremento (aumento) h y se encuentra un punto x + h.
Se traza la tangente a la curva en el punto de abscisa x, y desde x + h se levanta una paralela al eje de ordenadas hasta cortar a la curva y a la tangente.
Si α es el ángulo que forma la tangente con el eje X, tg α = f'(x) = AC/h
Diferencial de una función en un punto
Se define diferencial de una función y = f(x) en un punto x, y se simboliza por dy ó df(x), al producto f'(x)·h. Por tanto,
dy = df(x) = f'(x)·h
Propiedades de la diferencial
Primera propiedad:
La diferencial de una función en un punto depende de dos variables: el punto x elegido y el incremento h que se ha tomado.
Segunda propiedad:
Al ser dy = f'(x)·h = AC, la diferencia de una función en un punto es el incremento (aumento) de la ordenada de la tangente al aumentar en h un punto de abscisa x.
Tercera propiedad:
Si se considera la función y = f(x) = x, df(x) = dx = f'(x)·h = 1·h = h. Así, dx = h y se puede escribir
d(f(x)) = dy = f'(x)·dx, y pasando dx al primer miembro, dy/dx = f'(x).
Cuarta propiedad:
Puesto que:
| dy = f'(x) = | lim h ⟶ 0 | f(x + h) - f(x) | , |
| h |
de la noción de límite se deduce que cuando h es infinitamente pequeño, el cociente dy es prácticamente igual a [f(x + h) - f(x)]/h, y puesto que h = dx, dy es prácticamente igual a f(x + h) - f(x).
Es decir, dy ≈ f(x + h) - f(x). Esta propiedad permitirá sustituir dy por f(x + h) - f(x) cuando h es muy pequeño, con la seguridad de que el error cometido será mínimo.
Ejemplos de cálculos aproximados utilizando la diferencial
Ejemplo nº 1
Un móvil se mueve según la relación s = 5·t² + t, donde s representa el espacio recorrido medido en metros y t el tiempo medido en segundos.
Se quiere saber los metros que recorre el móvil en el tiempo comprendido entre 7 segundos y (7 + ⅓) segundos.
Desarrollo
Datos:
s = 5·t² + t
t₁ = 7 s
t₂ = (7 + ⅓) s
Solución
Diferenciando la expresión s = 5·t² + t,
ds = (10·t + 1)·dt
Por otro lado, dt = 7 + ⅓ - 7 = ⅓
Sustituyendo en la expresión de ds,
ds = (10·7 + 1)/3 = 23,66 metros
En la figura se observa que en realidad recorre algo más de 23,66 metros:
s = 5·(7 + ⅓)² + (7 + ⅓) - (5·7² + 7) = 24,18 m
Se ha cometido un error de 24,18 m - 23,66 m = 52 cm
Ejemplo nº 2
Calcular 3,05²
Solución
Para encontrar un resultado aproximado de 3,05² se considera la función y = x²
Diferenciando esta función, dy = 2·x·dx
Por la proximidad de 3,05 a 3 (5 centésimas) se calculará la diferencial en el punto de abscisa x = 3 y se llevará a la expresión de dy.
En este caso dx = 3,05 - 3 = 0,05
dyₓ ₌ ₃ = 2·3·0,05 = 0,30
Por tanto, aproximadamente, 3,05² = 9 + 0,30 = 9,30.
Si se calcula con exactitud el valor de 3,05² se obtiene 9,3025. Se observa que se ha cometido un error de 9,3025 - 9,30 = 0,0025, ¡25 diezmilésimas!
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).