Propiedades de los diferenciales. Ejemplos.
Idea intuitiva:
Queremos aplicar el concepto de derivada y pendiente que estudiamos en una variable a varias variables.
La idea básica consiste en coger un vector v y ver que pasa en la función según nos movemos en la recta dada por el punto que queremos estudiar y el vector, cuando el módulo del vector tiende a cero.
Es decir, lo que hacemos es convertir la función a una variable, cortándola por el plano vertical que pasa por la recta ya mencionada.
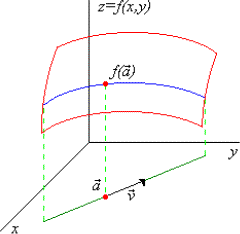
Gráfica para interpretar la diferencial de una función
Definición:
Sea f:U ⊂ ℜⁿ ⟶ ℜᵐ, ā, punto interior de U, y v ∈ ℜⁿ, v ≠ 0. Entonces llamamos derivada de f según el vector v a:
| Dᵥ f(ā) = | lim t ⟶ 0 | f(ā + t·v) - f(ā) |
| t |
Observación:
Si y ≠ 0, entonces:
Dλv f(ā) = λ·Dᵥ f(ā)
• Demostración:
| Dλv f(ā) = | lim t ⟶ 0 | f(ā + λ·t v) - f(ā) | · | λ | = |
| t | λ |
| Dλv f(ā) = λ· | lim t ⟶ 0 | f(ā + h·v) - f(ā) | = λ·Dᵥ f(ā) |
| t |
Notación: Sea x ∈ ℜⁿ. Entonces definimos la norma de x cómo:
|x| = √∑ᵢ²
Definición:
Llamaremos derivada direccional de f según una dirección definida por v a la derivada según el vector: ŭ = v/|| v||
Ejemplo nº 1
| f(x, y) = | x·y²/(x² + y⁴) | (x, y) ≠ (0, 0) |
| 0 | (x, y) = (0, 0) |
| Dᵥ f(0) = | lim t ⟶ 0 | f(0 + t·v) - f(0) | = |
| t |
| t³·cos θ·sen² θ | |||
| = | lim t ⟶ 0 | t²·cos² θ + t⁴·cos⁴ θ | = |
| t |
| t³·cos θ·sen² θ | |||
| = | lim t ⟶ 0 | t²·(cos² θ + t²·cos⁴ θ) | = |
| t |
| = | lim t ⟶ 0 | t³·cos θ·sen² θ | = |
| t·t²·(cos² θ + t²·cos⁴ θ) |
| = | lim t ⟶ 0 | cos θ·sen² θ |
| cos² θ + t²·cos⁴ θ |
| Dᵥ f(0) = | sen² θ/cos θ | cos θ ≠ (0, 0) |
| 0 | cos θ = (0, 0) |
Existen todas las derivadas direccionales de f, pero f no es contínua en (0, 0)
Si hacemos x = m·y²
| lim y ⟶ 0 | f(m·y², y) = | lim y ⟶ 0 | m·y⁴ |
| m·y⁴ + y⁴ |
| lim y ⟶ 0 | f(m·y², y) = m/(m + 1) |
Luego el límite no existe y la función no es contínua.
Observación:
Si f = (f₁, …, fₘ): ℜⁿ ⟶ ℜᵐ, entonces:
Dᵥ f(ā) = (Dᵥ f₁(ā), …, Dᵥ fₘ(ā))
Definición:
Sea f:U ⊂ ℜⁿ ⟶ ℜᵐ, ā, punto interior de U. Entonces llamamos derivada parcial respecto de xᵢ, i = 1, …, m a la derivada direccional de f según el vector ē de la base canónica de ℜᵐ. Lo representamos de la siguiente manera:
Dē, f = ∂f/∂xᵢ
Ejemplo nº 2
f(x, y) = x·ex² + y²
∂f/∂x = (1 - 2·x²)·ex² + y²
∂f/∂y = 2·x·y·ex² + y²
Definición:
Sea f:U ⊂ ℜⁿ ⟶ ℜᵐ, U abierto. Entonces se dice que f es diferenciable en ā ∈ U si existe una aplicación lineal Df(ā):U ⊂ ℜⁿ ⟶ ℜᵐ, que llamaremos diferencial de f en ā, tal que:
| lim h ⟶ ū | f(ā + h) - f(ā) - [Df(ā)](h) | = 0 |
| ||h|| |
Pedimos que el numerador, que es el error que cometemos al aproximar f(ā+ h) = f(ā) + [Df(ā)](h), sea una "o pequeña" de h, de tal manera que tiende más rápidamente a 0 que h. Es decir, pedimos que el error tienda a cero.
Observación:
Debido al carácter vectorial de las funciones de varias variables, podemos tratarlas en un plano algebraico, y aplicar en ellas todo lo que sabemos acerca de representación matricial de homomorfismos
Ejemplo nº 3
f(x, y) = (x² + y²)½
¿Existe Df(Ō)?
M(Df, Bc) = A = (α, β)
h = (h, k)
| [Df(Ō)](h) = (α β)·( | h | ) = α·h + β·k |
| k |
| ¿∃ α,β ∈ ℜ / | lim (h, k) ⟶ (0, 0) | f[(0,0) + (h,k)] - f(0,0) - (α·h + β·k) | = 0? |
| ||h|| |
| lim (h, k) ⟶ (0, 0) | f[(0,0) + (h,k)] - f(0,0) - (α·h + β·k) | = |
| ||h|| |
| = | lim (h, k) ⟶ (0, 0) | √h² + k² - α·h - β·k | = |
| √h² + k² |
Acercándonos por h = 0:
| lim k ⟶ 0 | √k² - β·k | = | lim k ⟶ 0 | |k| - β·k | = f(β) |
| √k² | |k| |
| f(β) | 1 ⟶ β = 0 ∄ ⟶ β ≠ 0 |
Y por k = 0
| lim h ⟶ 0 | √h² - α·h | = | lim h ⟶ 0 | |h| - α·h | = f(α) |
| √h² | |h| |
| f(α) | 1 ⟶ α = 0 ∄ ⟶ α ≠ 0 |
Luego la función no es diferenciable.
Autor: José Luis Martínez-Avila. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).