Propiedades de los diferenciales. Ejemplos.
Idea intuitiva:
Veamos una interpretación geométrica de la diferencial, para el caso de n = 2.
Sea x = (x, y) (pequeño), y f diferenciable en ā = (a, b), [Df(ā)](x) = α·x + β·y para ciertos α y β ∈ ℜ. Entonces:
f(ā + x) = f(ā) + α·x + β·y + 0(||x||)
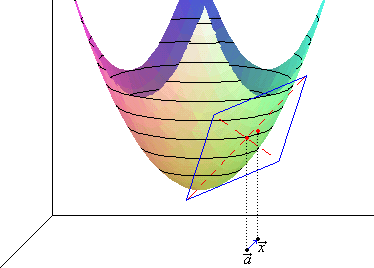
Puedo hacer f(ā + x) igual a la función en ā más el plano en un punto (x, y) tangente en ā, más un error pequeño.
Por tanto, si se cumplen las condiciones anteriores, llamamos plano tangente a una superficie z = f(x, y) en el punto (a, b, f(ā)) al plano z = α·x + β·y
Propiedades:
1) Si f: ℜⁿ ⟶ ℜᵐ es diferenciable en ā, entonces la diferencial es única
2) f = (f₁, …, fₘ): ℜⁿ ⟶ ℜᵐ es diferenciable en ā si y solo si fᵢ es diferenciable en ā i = 1, …, m. Además la diferencial es:
Df(ā) = (D₁ f(ā), …, Dₘ f(ā))
3) Si f, g: ℜⁿ ⟶ ℜᵐ son diferenciadles en ā, entonces λ·f, λ ∈ ℜ, f ± g, f·g, (m = 1) son diferenciadles en ā, y se verifica:
a) D(λ f)·(ā) = λ Df(ā)
b) D(f ± g)·(ā) = Df(ā) ± Dg(ā)
c) D(f. g)·(ā) = Df(ā). g(ā) + f(ā)·Dg(ā)
• Proposición:
Sea f:U ⊂ ℜⁿ ⟶ ℜᵐ. Si f es diferenciable en ā ∈ U, entonces existe D ᵥ f(ā), ∀ v ≠ 0, y además Dv f(ā) = [Df(ā)](v)
• Demostración:
| Dv f(ā) = | lim t ⟶ 0 | f(ā + t·v) - f(ā) | = | lim t ⟶ 0 | [Df(ā)] + o((||t·v||)) |
| t | t |
| Dv f(ā) = | lim t ⟶ 0 | t·[Df(ā)](v) + o(|t|·||t·v||) | = [Df(ā)](v) |
| t |
Observación:
Sea f:ℜⁿ ⟶ ℜ, y h = ∑hᵢ·ē. Entonces:
[Df(ā)](h) = [Df(ā)](∑hᵢ·ēᵢ)
[Df(ā)](h) = ∑hᵢ·[Df(ā)](ēᵢ)
[Df(ā)](h) = ∑hᵢ·[Dēif(ā)]
[Df(ā)](h) = ∑(∂f/∂xᵢ)(ā)·hᵢ
Definición:
Sea f:ℜⁿ ⟶ ℜ. Entonces llamamos vector gradiente de f en ā a:
| ∇f(ā) = [ | ∂f | (ā), …, | ∂f | (ā)] |
| ∂x₁ | ∂xₘ |
Observación:
1) Si f es diferenciable en ā, entonces Dv f(ā) = [Df(ā)](v) = ∇ f(ā) v
2) ∇. v = ||∇f||·|| v||·cos α = (Si v es unitario) = ||∇f||·cos α. Dicha expresión es máxima cuando v tienen la dirección del gradiente. Como el gradiente nos da el crecimiento de la función, deducimos que el vector gradiente tiene la dirección de máximo crecimiento de la función
• Proposición:
Una función derivable direccionalmente puede no ser diferenciable.
Ejemplo una función derivable direccionalmente que no es diferenciable
| f(x, y) = | x·y²/(x² + y⁴) | (x, y) ≠ (0, 0) |
| 0 | (x, y) = (0, 0) |
Está función es derivable direccionalmente, pero no es diferenciable. Estudiando la diferencial por la definición:
| ∂f | (0, 0) = | lim t ⟶ 0 | f(0 + t·0) - f(0, 0) |
| ∂x | t |
| ∂f | (0, 0) = | lim t ⟶ 0 | 0 - 0 |
| ∂x | t |
| ∂f | (0, 0) = 0 |
| ∂x |
| ∂f | (0, 0) = | lim t ⟶ 0 | f(0 + t·0) - f(0, 0) |
| ∂y | t |
| ∂f | (0, 0) = | lim t ⟶ 0 | 0 - 0 |
| ∂y | t |
| ∂f | (0, 0) = 0 |
| ∂y |
Luego si f fuera diferenciable, su diferencial sería cero
| ¿ | lim h ⟶ 0 k ⟶ 0 | f(0 + h, 0 + k) - f(0,0) - [Df(Ō)](h,k) | = 0? |
| √h² + k² |
| h·k² | ||
| lim h ⟶ 0 k ⟶ 0 | h² + k⁴ | = ∄ |
| √h² + k² |
Luego la función no es diferenciable.
Definición:
Sea f: ℜⁿ ⟶ ℜᵐ diferenciable en ā. Entonces a la matriz asociada a la aplicación D f(ā) en las bases canónicas de ℜⁿ y ℜᵐ se le llama matriz jacobiana de f en ā, y se denota J f(ā)
Observación:
Estudiemos como es la matriz. Si f = (f₁, …, fₘ), tomamos ē₁ ∈ ℜⁿ. Las coordenadas de su imagen son la primera columna de la matriz:
[Df(ā)](ē₁) = Dē1f(ā)
| [Df(ā)](ē₁) = | ∂f | (ā) |
| ∂x₁ |
| [Df(ā)](ē₁) = [ | ∂f₁ | (ā),…, | ∂fₘ | (ā)] |
| ∂x₁ | ∂x₁ |
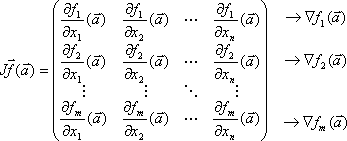
Ejemplo: Calcular la matriz jacobiana de la siguiente aplicación:
Sea A = [0, +∞]x(0, 2·π] ⊂ ℜ² y g(r, θ) = (r, cos θ, r·sen θ))
| Jf(ā) = | ∂g₁ | ·(ā) | ∂g₁ | ·(ā) | ||
| ∂r | ∂θ | |||||
| ∂g₂ | ·(ā) | ∂g₂ | ·(ā) | |||
| ∂r | ∂θ |
| Jf(ā) = | cos θ | -r·sen θ | ||
| sen θ | r·cos θ |
• Proposición:
Si f:U ⊂ ℜⁿ ⟶ ℜᵐ es diferenciable en ā, entonces es contínua en ā
• Demostración:
La haremos para f:ℜⁿ ⟶ ℜ
Hay que demostrar que:
| lim h ⟶ ū | f(ā + h) = f(ā) ⇔ | lim h ⟶ ū | [f(ā + h) - f(ā)] = 0 |
Como f es diferenciable en ā
f(ā + h) - f(ā) = [Df(ā)](h) + o(||h||)
| lim h ⟶ ū | [f(ā + h) - f(ā)] = |
| = | lim h ⟶ ū | [Df(ā)](h) + o(||h||) = |
| = | lim h ⟶ ū | [Df(ā)](h) = |
| = | lim h ⟶ ū | [ | ∂f | ·(ā)·h₁ + … + | ∂f | ·(ā)·hₙ] = 0 |
| ∂x₁ | ∂xₙ |
Definición:
Sea f:U ⊂ ℜⁿ ⟶ ℜᵐ, U abierto. Decimos que f es de clase C¹ en ā ∈ U si todas las derivadas parciales de f están definidas en un entorno de ā y además son continuas en ā.
Por consiguiente f es de clase C¹ en U si lo es en todos los puntos de U
Teorema:
Si f:U ⊂ ℜⁿ ⟶ ℜᵐ es de clase C¹ en ā, entonces es diferenciable en ā
Observación:
En general, el recíproco no es cierto.
Autor: José Luis Martínez-Avila. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
¿Qué es el gradiente y qué representa?