Problema nº 1-h de ecuaciones de primer grado, despejar "x" - TP03

Enunciado del ejercicio nº 1-h

Resolver la siguiente ecuación hallando el valor de "x":

Solución

Antes de comenzar observamos los denominadores, sabemos que para que la ecuación tenga solución ningún denominador puede ser igual a cero, por lo tanto:

x ≠ ±2

Sumamos las fracciones, para calcular el común denominador tendremos en cuenta que:

x² - 4 = (x - 2)·(x + 2)

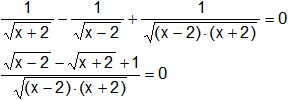
Pasamos el denominador del otro lado del "=" multiplicando por cero:

Elevamos amobos términos al cuadrado:

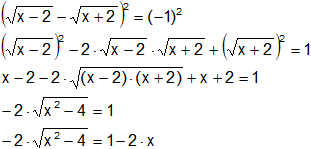
Elevamos amobos términos al cuadrado:

4·(x² - 4) = (-2·x + 1)²

4·x² - 4·4 = 4·x² - 4·x + 1

4·x² - 16 = 4·x² - 4·x + 1

Cancelamos:

4·x² - 16 = 4·x² - 4·x + 1

-16 = -4·x + 1

Despejamos "x" y obtenemos el resultado:

4·x = 16 + 1

4·x = 17

x = 17/4

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP03
• | Siguiente ›

Ejemplo, cómo resolver ecuaciones de primer grado. Despejar "x".