Intervalo de confianza
1) Para la media μ de una población normal:
Li/s = x ± zα/2·σ/√n
Tener en cuenta que una confianza del 95 % significa:
α/2 = 0,95
p = 1 - q
p = x/n
2) Para la media X:
Li/s = x ± t(n - 1)·(1 - α/2)·S/√n
t(α, v) se busca en tabla.
3) Para la varianza S²:
X²(α, v) se busca en tabla.
4) Para el desvío estándar S:
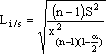
5) Para muestras grandes:
Un intervalo de confianza 100(1 - α)% para la proporción p de una población, de muestras grandes, es:
p ± zα/2√p·q/n
Dónde p = x/n, n tamaño muestral, x es el número observado de éxitos, y q = 1 - p.
Este intervalo se puede emplear siempre que n·p ≥ 5 y n·q ≥ 5.
Ejemplo: El gerente financiero de una gran cadena de tiendas seleccionó una muestra aleatoria de 200 de sus clientes que utilizan tarjetas de crédito, y encontró que 136 habían incurrido en cargos por intereses durante el año anterior debido a falta de pago de sus saldos.
a) Calcule un intervalo de confianza de 95% para la verdadera proporción de clientes que utilizan tarjetas de crédito, quienes han incurrido en cargos por intereses durante el año anterior
b) Si la longitud deseada del intervalo de 90% es 0,05, ¿qué tamaño muestral es necesario para asegurar esto?
c) Calcule el intervalo de confianza de 82% para la verdadera proporción
n = 200
x = 136
a)
Para 1 - α/2 = 0,95
p = x/n
p = 136/200 = 0,68
p = 1 - q ⇒ q = 1 - p
q = 1 - 0,68 = 0,32
Li/s = p ± z(1 - α/2)·√p·q/n
Li/s = 0,68 ± z(0,95)·√0,68·0,32/200
De tabla z(0,95) = 1,645
Li/s = 0,68 ± 1,645·0,33
Li/s = 0,68 ± 0,054
(0,626; 0,734)
b)
n = [z(1 - α/2)²·p·q]/L²
n = 1,645²·0,5·0,5/(0,25²)
Sin sondeo previo tomar p = q = 0,5
n = 10,82 clientes
c)
Para el 82 %
Li/s = p ± z(1 - α/2)·√p·q/n
α = 0,82
1 - α = 0,18
α/2 = 0,09
1 - α/2 = 0,91
De tabla e interpolando z(1 - α/2) = 1,3425
Li/s = 0,68 ± z(0,91)·√0,68·0,32/200
De tabla z(0,91) = 1,645
Li/s = 0,68 ± 1,3425·0,33
Li/s = 0,68 ± 0,0443
(0,6357; 0,7243)
Bibliografía:
"Probabilidad y estadísticas para ingeniería y ciencias". Jay L. Devore. 1.998.
Autor: Ricardo Santiago Netto (Administrador de Fisicanet)
San Martín. Buenos Aires. Argentina.
Ver condiciones para uso de los contenidos de fisicanet.com.ar