Cálculo de probabilidades
La expansión del cultivo de soja en la Argentina es objeto de una fuerte controversia entre quienes aprecian las ventajas económicas actuales de dicha expansión y quienes alertan sobre problemas de contaminación ambiental, de empobrecimiento cultural y de fragilidad de la economía asociados con ella. En parte, los problemas mencionados son característicos del monocultivo y ya han ocurrido en regiones donde el cultivo hegemónico era otro.
Nuestro problema será encontrar una manera para evaluar en qué medida la adopción del cultivo de soja está asociada con la práctica del monocultivo a partir de los datos de una encuesta en la cual se registran los cultivos realizados en los diferentes establecimientos agrícolas de un área determinada. Para ello utilizaremos las herramientas conceptuales y metodológicas que la estadística provee para realizar una evaluación de este tipo.
Problema (datos ficticios)
En un estudio de la actividad agrícola en un partido de la Pampa Ondulada se registraron los cultivos estivales de cosecha realizados en la última campaña en 100 establecimientos elegidos al azar dentro del partido. La planilla que llevaban los encuestadores permitía registrar las siguientes opciones: Maíz, Girasol, Sorgo, Soja, Cártamo. Entre los resultados de la encuesta se encontró que en 90 de los 100 establecimientos relevados se había cultivado soja y que, en 40 de ellos, la soja era el único cultivo estival; además, 2 establecimientos realizaron otro tipo de monocultura (datos ficticios).
• Identificar la población bajo estudio
• Identificar la muestra
• Detallar las 31 diferentes posibilidades para la lista de los cultivos realizados en un establecimiento (los 31 eventos simples que componen el espacio muestral)
• Indicar cuáles eventos simples componen los siguientes eventos compuestos:
∘ "en el establecimiento se cultivó soja",
∘ "en el establecimiento de cultivó maíz y girasol",
∘ "el establecimiento realizó un único cultivo estival",
∘ "en el establecimiento se realizaron más de 3 cultivos diferentes"
Definiciones
• Probabilidad: Es un valor comprendido entre 0 y 1, incluidos estos dos valores, que describe la posibilidad de ocurrencia de un evento
• Experimento: Cualquier proceso que produce un resultado
∘ Determinístico: Ante la repetición del mismo se obtiene siempre el mismo resultado
∘ Aleatorio: Repitiendo el experimento en idénticas condiciones se obtienen distintos resultados
• Punto muestral ó resultado: Es un resultado particular de un experimento
• Evento: Es una colección de uno o más resultados de un experimento
Definiciones evento o suceso aleatorio
• Evento o Suceso Aleatorio: Es una colección de uno o más resultados de un experimento
∘ E1 = Sacar un 5 al tirar un dado
∘ E2 = Sacar un número par al tirar un dado
∘ E3 = Sacar un número menor que 7 al tirar un dado = Evento cierto
∘ E4 = Sacar un número mayor que 6 al tirar un dado = Evento imposible
Definiciones sucesos compuestos
• Sucesos mutuamente excluyentes:
∘ Dos sucesos A y B son mutuamente excluyentes cuando la ocurrencia de uno de ellos impide la ocurrencia del otro
∘ P(A∩B) = P(A y B) = P(AB) = 0
• Sucesos colectivamente exhaustivos
∘ Dos sucesos A y B son colectivamente exhaustivos cuando al menos uno de ellos deba ocurrir siempre que se realiza el experimento
∘ Dicho en otras palabras, deberá cumplirse que la suma de las probabilidades de todos los sucesos deberá ser igual a 1
Definiciones espacio muestral
• Espacio muestral: Es el conjunto de todos los posibles resultados de un experimento.
• Suele representarse con la letra S. Puede visualizarse a través de:
▫ Listas
∘ Conjunto de posibles resultados al tirar un dado = {1; 2; 3; 4; 5; 6}
▫ Diagramas de arbol
Conjunto de posibles resultados al tirar dos monedas
| C | ||
| C | ❬ | |
| S | ||
| C | ||
| S | ❬ | |
| S |
• Tablas rejilla
- Conjunto de posibles resultados al tirar un dado rojo y uno azul
| 11 12 13 14 15 16 | 21 22 23 24 25 26 | 31 32 33 34 35 36 | 41 42 43 44 45 46 | 51 52 53 54 55 56 | 61 62 63 64 65 66 |
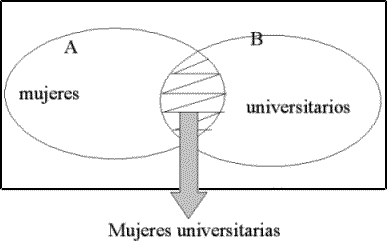
• Conjuntos (Diagramas de Venn)
- Se pretende representar a las mujeres, a los universitarios pero es necesario tener en cuenta que existen mujeres universitarias.
• Tablas de doble entrada
- Cuando se tienen dos o más variables con dos o más categorías cada una, por ejemplo hombres y mujeres, Ingenieros Agrónomos y Licenciados en Economía y Administración Agraria.
| Ingenieros Agrónomos | Licenciados en Economía y Administración | ||
| M | 40 | 25 | 65 |
| H | 60 | 30 | 90 |
| 100 | 55 | 155 |
Recordemos cuales son los totales marginales y el gran total.
Definiciones de probabilidad
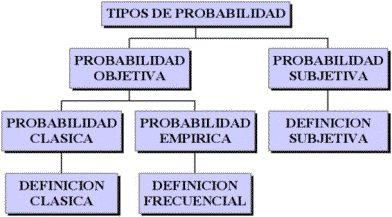
• Definición clásica
• Se basa en que todos los resultados son:
∘ Igualmente probables o equiprobables
∘ Mutuamente excluyentes
∘ Colectivamente exhaustivos
| Probabilidad de un evento = | Número de resultados favorables |
| Número de resultados posibles |
• Definición frecuencial
Cuando los resultados no son equiprobables la probabilidad de ocurrencia de un evento se determina por observación del número de veces que eventos similares ocurrieron en el pasado. (frecuencia relativa)
| Probabilidad de un evento = | Número de veces que el evento ocurrió en el pasado |
| Número de observaciones |
Ejemplo nº 1
Sea el experimento de estudiar una droga que cura cierta enfermedad en vacunos enfermos. Se aplicó a 1.000 vacunos y se curaron 700.
- El espacio muestral será S = {curado; no curado}
- Consideremos el evento de que el vacuno se cure
- Probabilidad de curado = 700/1.000 = 0,7
• Definición subjetiva
Cuando no se tienen datos para ningún tipo de cálculo, ni posibilidad de efectuar repetidamente el experimento, se recurre a un experto, quien de acuerdo a su buen saber y entender estimará la probabilidad.
Ejemplos:
- Calcular la probabilidad de que un tenista gane un campeonato
- Calcular la probabilidad de que un club de futbol salga campeón
- Calcular la probabilidad de que el precio de las acciones de una compañía se incremente en dos años
Axiomas de probabilidades
Independientemente de que definición de probabilidad utilicemos, siempre se deberán cumplir los siguientes tres axiomas.
Axiomas:
• Axioma 1: La probabilidad de un evento existe y es un número mayor o igual a cero.
0 ≤ P(A)
• Axioma 2: La probabilidad de todo el espacio muestral es 1.
P(S) = 1
• Axioma 3: Si dos eventos A y B son mutuamente excluyentes.
P(A∪B) = P(A) + P(B)
Consecuencias de los axiomas de probabilidades
P(Φ) = 0
Si Ā = suceso complementario de A es decir Ā = S - A, será P(Ā) = 1 - P(A)
Si A1 ⊂ A2, entonces P(A1) ≤ P(A2)
"A se cumple que P(A) ≤ 1
Regla general de la suma
Si A y B son dos sucesos no mutuamente excluyentes, luego la probabilidad de la unión entre ambos está dada por la siguiente fórmula.
P(A∪B) = P(A) + P(B) - P(A∩B)
| B | ||
| A | A y B | |
Si A y B son dos sucesos mutuamente excluyentes, se cumple:
P(A∪B) = P(A) + P(B)
Ejemplo nº 2
Un experimento genera un espacio muestral que contiene ocho sucesos E1, …, E8 con p(Ei) = ⅛, i = 1, …, 8. Los sucesos A y B se definen así:
A = {E1, E4, E6}
B = {E3, E4, E5, E6, E7}
Encuentre:
a) P(A)
b) P(Ā)
c) P(A∪B)
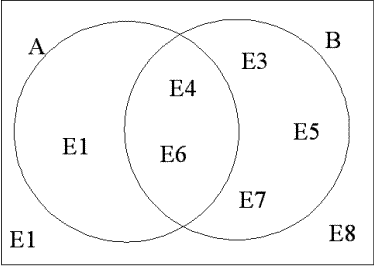
a. P(A) = ⅜
b. P(Ā) = ⅝
c. P(A∪B) = P(A) + P(B) - P(A∩B)
P(A∪B) = ⅜ + ⅝ - 2/8 = 6/8 = 0,75
Resultado que es muy fácil verificar visualmente en el diagrama.
Independencia
Dos eventos A y B son independientes cuando se cumple que la probabilidad conjunta es igual al producto de las probabilidades marginales.
P(A∩B) = P(A)·P(B)
Probabilidad condicional
Probabilidad Condicional es la probabilidad de ocurrencia de un evento en particular, dado que otro evento ha ocurrido. La probabilidad condicional del evento A dado que el evento B ha ocurrido se escribe P(A|B).
Regla general del producto
Dados dos eventos A y B la probabilidad conjunta de que ambos sucedan se calcula según la siguiente fórmula:
P(A∩B) = P(A)·P(B|A) = P(B∩A) = P(B)·P(A|B)
Si los eventos A y B son independientes la probabilidad conjunta de que ambos sucedan se calcula según la siguiente fórmula:
P(A∩B) = P(B∩A) = P(A)·P(B) = P(B)·P(A)
Ejemplo nº 3
Un experimento genera un espacio muestral que contiene ocho sucesos E1, …, E8 con p(Ei) = ⅛, i = 1, …, 8. Los sucesos A y B se definen así:
A = {E1, E4, E6}
B = {E3, E4, E5, E6, E7}
Resolver:
a) ¿Son los sucesos A y B mutuamente excluyentes? ¿Por qué?
b) ¿Son los sucesos A y B independientes? ¿Por qué?
c) P(A∩B)
d) P(A|B)
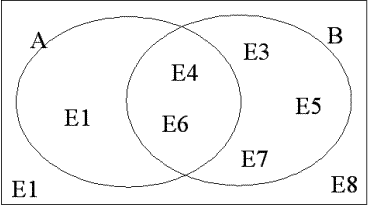
a)
No, porque A ∩ B ≠ 0
b)
No, porque P(A)·P(B) ≠ P(A∩B)
⅜·⅝ ≠ 2/8
c)
P(A∩B) = 2/8 = 0,25
d)
P(A|B) = P(A∩B)/P(B) = (2/8)/(⅝) = ⅖
Esto puede verse en el diagrama, ya que saber que B ocurrió, reduce nuestro espacio muestral a los cinco elementos de B. Y de ellos, sólo dos pertenecen a A.
Problemas a resolver
Ejercicio nº 1
Dos candidatos a los consejos de administración A y B, compiten por el control de una corporación. Las probabilidades de ganar de estos candidatos son 0,7 y 0,3, respectivamente. Si gana A, la probabilidad de introducir un nuevo producto es 0,8; si gana B, la correspondiente probabilidad es 0,4. Demuestre que, antes de las elecciones, la probabilidad de que sea introducido un nuevo producto es 0,68.
Sugerencias: Recordar probabilidad condicional y probabilidad conjunta Considerar todo el espacio muestral.
Desarrollo
Datos:
P(A) = 0,7
P(N|A) = 0,8
P(B) = 0,3
P(N|B) = 0,4
Fórmulas:
P(N) = P(N∩A) + P(N∩B)
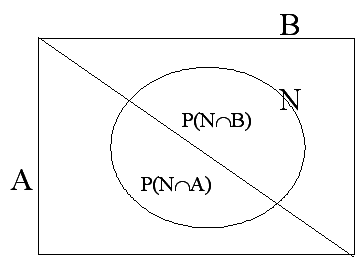
Solución
P(N) = P(N|A)·P(A) + P(N|B)·P(B)
P(N) = 0,8·0,7 + 0,4·0,3 = 0,68
Ejercicio nº 2
El 34 % de los árboles de un bosque tienen más de 15 años. El 54 % son de la variedad A. De los de la variedad A, el 7 % tiene más de 15 años. Si se elige un árbol al azar,
a) ¿Cuál es la probabilidad de que tenga más de 15 años y sea de la variedad A?
b) ¿Cuál es la probabilidad de que teniendo menos de 15 años, sea de la variedad A?
Sugerencias: Recordar probabilidad condicional y probabilidad conjunta. Considerar tablas de contingencia.
| +15 | -15 | ||
| A | 0,0378 | 0,5022 | 0,54 |
| Ā | 0,3022 | 0,1578 | 0,46 |
| 0,34 | 0,66 | 1 |
Solución
a) P(+15∩A) = P(+15|A)·P(A) = 0,07·0,54 = 0,0378
b) P(A|-15) = P(A∩-15)/P(-15) = 0,5022/0,66 = 0,76
Ejercicio nº 3
El 70 % del ganado es inyectado con una vacuna para combatir una enfermedad grave. La probabilidad de recuperarse de la enfermedad es 1 en 20 si no ha habido tratamiento y de 1 en 5 si hubo tratamiento. Si un animal infectada se recupera, ¿cuál es la probabilidad de que haya recibido la vacuna preventiva?
Sugerencias: Recordar probabilidad condicional y probabilidad conjunta. Regla del producto.
Desarrollo
Datos:
P(I) = 0,7
P(R|I) = 0,2
P(Ī) = 0,3
P(R|Ī) = 0,05
Fórmulas:
P(I|R)
Solución
Incógnita:
| P(I|R) = | P(I∩R) |
| P(R) |
| P(I|R) = | P(I∩R) |
| P(I∩R) + P(R∩Ī) |
| P(I|R) = | P(I|R)·P(I) |
| P(R|I)·P(I) + P(R|Ī)·P(Ī) |
| P(I|R) = | 0,2·0,7 |
| 0,2·0,7 + 0,05·0,3 |
P(I|R) = 0,9
Autor: Olga Susana Filippini. Argentina.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
¿Qué es una variable aleatoria discreta y continua? ¿Cuáles son las reglas de la probabilidad?