Variable aleatoria
Dado un experimento aleatorio y su correspondiente espacio muestral se denomina variable aleatoria a la función que asigna a cada elemento del espacio muestral un número real.
X: S ⟶ ℜ/X(s) x
Ejemplo: Si se define la variable aleatoria X = número de caras obtenidas al arrojar dos monedas
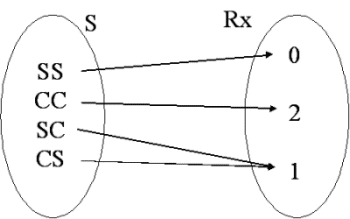
¿Qué valores puede tomar x?
X(SS) = 0
X(CS) = X(SC) = 1
X(CC) = 2
Se denomina recorrido Rx al conjunto de valores que puede tomar la variable.
Variable aleatoria discreta
Una variable aleatoria es discreta cuando toma un número contable de valores. Entonces entre dos valores consecutivos de una variable aleatoria discreta no hay ningún número que pertenezca al recorrido de la variable
Rx = {X1, X2, …, Xn, …} donde cada Xi es un valor de la variable aleatoria.
En general, estos valores no serán igualmente probables, sino que cada X tendrá asignada una probabilidad.
Luego, para caracterizar una variable aleatoria discreta es necesario conocer su recorrido y la probabilidad de cada elemento del recorrido
Sigamos con el ejemplo X = cantidad de caras al tirar dos monedas
P(X = 0) = P(SS) = ¼
P(X = 1) = P(SC; CS) = ½
P(X = 2) = P(CC) = ¼
Función de distribución de probabilidad
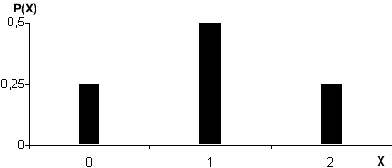
Propiedades:
1) P(Xᵢ) ≥ 0 ∀ Xᵢ
| 2) | ∑ Xᵢ ∈ Rᵢ | P(xᵢ) = 1 |
Variable aleatoria contínua
Una variable es contínua en un intervalo cuando puede tomar cualquier valor perteneciente al intervalo.
En general definiremos variables aleatorias continuas cuando las experiencias consistan en medir peso, altura, longitud, tiempo, temperatura, etc.
En este caso se define (en lugar de la función de distribución) una función de densidad de probabilidad que tiene las siguientes propiedades
1) f(x) ≥ 0 ∀ X ε R
| 2) ∫ | +∞ | f(x)·dx = 1 |
| -∞ |
| 3) a < b ⇒ P(a ≤ x ≤ b) = ∫ | a | f(x)·dx |
| b |
Esperanza de una variable aleatoria
La esperanza es un parámetro de la distribución. Es una medida de tendencia central.
Si X es discreta:
| μ = E(X) = | ∑ Xᵢ ∈ Rᵢ | xᵢ·p(xᵢ) |
Si X es contínua.
μ = E(X) = ∫ x·f(x)·dx
La esperanza E(x) no es un resultado que esperararíamos cuando X se observa sólo una vez.
Pero si observáramos un gran número de observaciones independientes de X el promedio de esos resultados estará cerca de E(x).
Ejemplo
En una operación comercial se puede obtener una utilidad de $1.000 o sufrir una pérdida de $500. Si la probabilidad de una utilidad es de 0,6, demuestre que la utilidad esperada en dicha operación es de $400.
Solución
Primero definimos la variable aleatoria.
X = utilidad en operación comercial
| μ = E(X) = | ∑ Xᵢ ∈ Rᵢ | xᵢ·p(xᵢ) |
E(X) = 1.000·0,6 + (-500)·0,4
E(X) = 400
Propiedades de la esperanza
Sean X e Y variables aleatorias y c una constante perteneciente a los reales:
1) E(c) = c
2) E(X + c) = E(X) + c
3) E(c·X) = c·E(X)
4) E(X + Y) = E(X) + E(Y)
5) E(X - Y) = E(X) - E(Y)
6) Si X e Y son independientes E(X·Y) = E(X)·E(Y)
Variancia de una variable aleatoria
La variancia es un parámetro de la distribución. Es una medida de dispersión de los valores de x alrededor de E(X)
Var(X) = σ² = E(X - μ)²
Var(X) = σ² = E(X² - [E(X)]²)
Propiedades de la variancia
Sean X e Y variables aleatorias y c una constante perteneciente a los reales:
1) V(c) = 0
2) V(X + c) = V(X)
3) V(c·X) = c²·V(X)
4) Si X e Y son independientes V(X + Y) = V(X) + V(Y)
5) Si X e Y son independientes V(X - Y) = V(X) + V(Y)
Teorema de Bayes
| P(A₁|B) = | P(A₁)·P(B|A₁) |
| P(A₁)·P(B|A₁) + P(A₂)·P(B|A₂) |
Repasando conceptos de conteo
• Permutaciones: Algunos arreglos de r objetos seleccionados de n posibles objetos
▫ n·Pᵣ = n!/(n - r)
• Nota: El orden de los arreglos es importante en las permutaciones
• Combinaciones: El número de formas de elegir r objetos de un grupo de n objetos sin considerar el orden
▫ n·Cᵣ = n!/r!·(n - r)
Autor: Olga Susana Filippini. Argentina.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
¿Qué es una variable aleatoria discreta y continua?