Inferencia estadística-hipótesis (segunda parte)
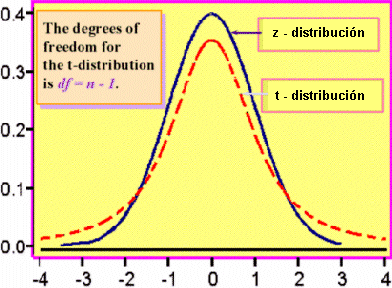
Características de la distribución t-Student
Tiene las siguientes propiedades:
∘ Es contínua, campanular, y simétrica como la distribución z
∘ Existe una familia de distribuciones t con media cero, pero con diferentes desviaciones estándar
∘ La distribución t es más aplanada y de colas más larga que la z
∘ Tiende a la z para tamaños grandes de muestra
Caso 1: Prueba de hipótesis para la media de una población
Supongamos que una máquina empacadora de harina produce bolsas con un contenido de 50 kg. Para controlar el funcionamiento de la máquina se tomó una muestra de 20 bolsas de harina y el peso medio resultó ser de 42 kg con un desvío standard de 11 kgs. ¿Está la máquina trabajando correctamente? (α = 0,10)
En este caso, se debe considerar que la máquina está trabajando correctamente si produce empaques que no excedan demasiado el peso promedio, ni por encima ni por debajo de 50 kgs, así que se trata claramente de una prueba bilateral.
Caso 1: Prueba de hipótesis para la media de una población, tamaño muestral pequeño y desviación estándar desconocida.
La estadística t para el caso de una sola muestra es:
t = (X - μ)/(s/√n)
Resolución
Hipótesis. H₀: μ = 50; H₁: μ ≠ 50
Nivel de significación. α = 0,10
Estadística de prueba. t₍ₙ ₋ ₁₎ = (X - μ)/(s₍ₙ ₋ ₁₎/√n)
Región crítica. Puesto que P(t₁₉ < -1,729 ∪ t₁₉ > +1,729) = 0,10, se rechazará H₀ si t < -1,729 ó t > +1,729
Cálculos. n = 20, = 42, = 5 y
t₁₉ = (42 - 50)/(11/√20) = -8/2,460 = -3,25
Decisión. Dado que el valor del estadístico de prueba cae netamente en la región crítica izquierda, H₀ es rechazada a favor de H₁
Valor P
- Valor p: probabilidad de observar un valor de prueba más extremo que el valor observado, dado que la hipótesi nula es verdadera
- Si el valor p es más chico que el nivel de significación la hipótesis nula es rechazada
- Si el valor p es más grande que el nivel de significación la hipótesis nula no es rechazada
Prueba de hipótesis para dos medias
Si un número grande de muestras aleatorias e independientes de dos poblaciones normales es seleccionada, la distribución de la diferencias entre las medias de ambas también es normal.
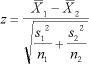
Caso 2: Prueba de diferencia entre medias con muestras independientes
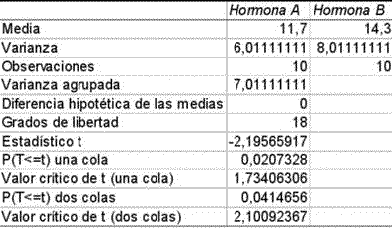
Un investigador estaba interesado en comparar el efecto de 2 hormonas (A y B) de crecimiento sobre la longitud total alcanzada por una leguminosa. Para ello se tomó una muestra de 20 plantas, asignando al azar 10 a cada hormona. Los resultados en cm fueron los siguientes:
| Hormona A: Hormona B: | 10 15 | 10 11 | 13 16 | 12 17 | 10 18 | 8 9 | 12 14 | 11 12 | 16 15 | 15 16 |
a) Determinar si hay diferencias significativas entre los crecimientos producidos por ambas hormonas a un nivel del 5 %.
b) Realizar el mismo análisis que en (a), pero suponiendo que cada una de las parejas, en el orden dado, tienen la misma ascendencia genética.
Solución
Prueba t para dos muestras suponiendo varianzas iguales
Caso 3: Muestras relacionadas
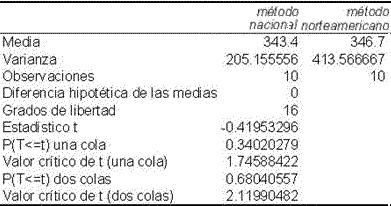
En un estudio para predecir a partir del perímetro torácico el peso de novillos de raza británica sin balanza, se compararon las evaluaciones hechas mediante una cinta métrica de origen norteamericano con los obtenidos mediante el pesado por método nacional. Las observaciones para cada animal fueron las siguientes:
| Novillo | Peso por método nacional | Peso por método norteamericano |
| 1 | 335 | 347 |
| 2 | 362 | 359 |
| 3 | 338 | 359 |
| 4 | 329 | 334 |
| 5 | 333 | 341 |
| 6 | 371 | 391 |
| 7 | 356 | 334 |
| 8 | 341 | 341 |
| 9 | 334 | 347 |
| 10 | 335 | 314 |
a) ¿Qué tipo de análisis sería correcto realizar? ¿Por qué? ¿Por qué cree que el experimento se diseñó de esa manera? ¿Cómo se debería haber hecho el experimento para que lo correcto fuera otro análisis?
b) ¿Cuáles son las hipótesis que se postulan? ¿Qué significa cada una de ellas?
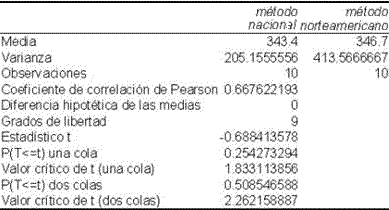
c) Utilizando un nivel de significación del 5 %, ¿cuál es la región de rechazo para el estadístico de prueba?
d) ¿A qué conclusión se llega? ¿En qué se basa dicha conclusión?
e) ¿Qué error se puede estar cometiendo al arribar a la conclusión anterior? ¿En qué consiste dicho error en términos de este problema?
f) Construya un intervalo del 95 % de confianza para estimar la diferencia promedio entre los dos preparados.
g) ¿Era de esperar que el intervalo cubriera o no el valor 0? ¿Por qué?
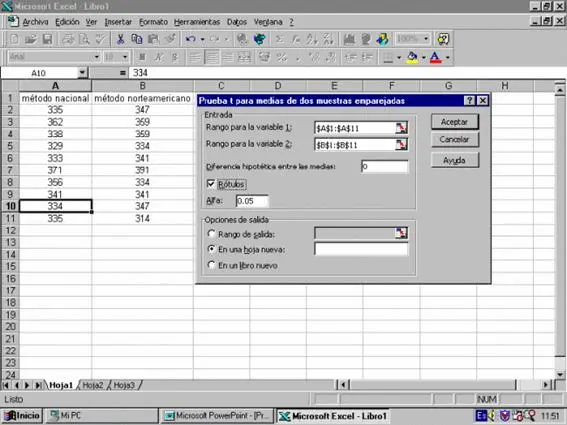
Prueba t para medias de dos muestras emparejadas
Prueba t para dos muestras suponiendo varianzas iguales
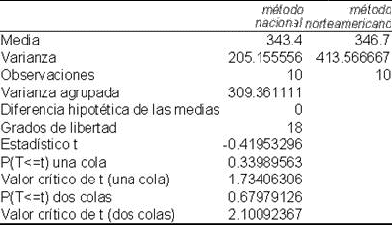
Prueba t para dos muestras suponiendo varianzas desiguales
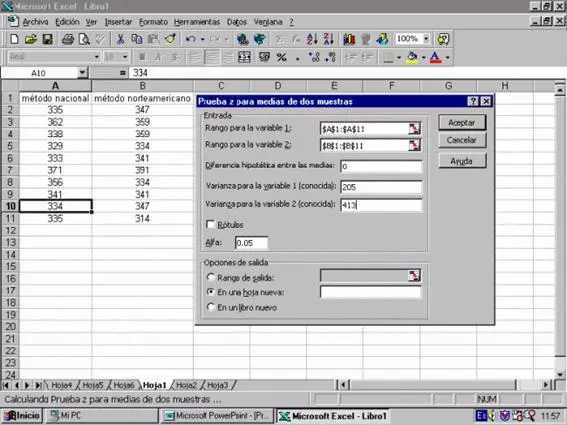
Prueba z para medias de dos muestras
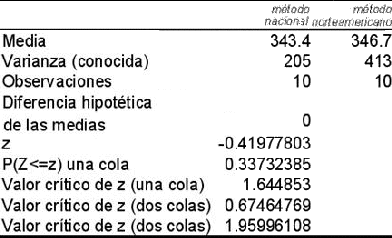
Análisis de variancia - caso de una sola variable. Varias muestras
Una compañía de alimentos envasados desea probar 4 nuevos diseños de empaques para un nuevo cereal para desayunos. Se seleccionaron 10 negocios con igual volumen de ventas como unidades experimentales. A cada negocio se le consignó al azar un diseño de empaque. Tres diseños de empaques se asignaron al azar a 3 negocios y el otro diseño fue asignado a dos negocios. Todas las otras condiciones ajenas al empaque, como precio, cantidad de estantes y localización de los mismos y esfuerzos especiales de promoción, se mantuvieron constantes (homogéneos) para todos los negocios del experimento. Las ventas, según número de casos, fueron registradas para el período de estudio y los resultados se presentan en la siguiente tabla:
Número de ventas por negocio para cada uno de los 4 diseños
| Diseño de empaques | Negocios, repetición | Total | N° de negocios | Media | ||
| 1 | 2 | 3 | ||||
| 1 | 12 | 18 | 3 | 33 | 3 | 11 |
| 2 | 14 | 12 | 13 | 39 | 3 | 13 |
| 3 | 19 | 17 | 21 | 57 | 3 | 19 |
| 4 | 24 | 30 | 24 | 78 | 3 | 26 |
| Total | 207 | 12 | 17,25 | |||
Análisis de varianza de un factor
Resumen
| Grupos | Cuenta | Suma | Promedio | Varianza |
| 1 2 3 4 | 3 3 3 3 | 33 39 57 78 | 11 13 19 26 | 57 1 4 12 |
Autor: Olga Susana Filippini. Argentina.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
- ‹ Anterior
- |
- Siguiente ›
¿Qué es la prueba de chi cuadrado? ¿Qué es la distribución t de Student?