Problema nº 1 de regresión lineal - TP04
Enunciado del ejercicio nº 1
En una estación experimental de Rafaela, Santa Fe se realizó un ensayo para evaluar el efecto del nivel de suplementación con alimento balanceado (kg/día/animal) sobre la producción de leche (Lts/día/animal) en vacas Holando-Argentino. En las siguientes tablas y figuras se resumen los resultados obtenidos de un análisis de regresión lineal efectuado por los investigadores que condujeron el estudio.
Análisis de regresión lineal
| Variable | N | R² |
| Leche | 9 | 0,93 |
Matriz de coeficientes de regresión
| Coeficiente | Estimado | Error | LI (95 %) | LS (95 %) | T | p |
| Intercepción Pendiente | 17,87 1,45 | 0,73 0,15 | 16,14 1,09 | 19,59 1,81 | 24,51 9,47 | < 0,001 < 0,001 |
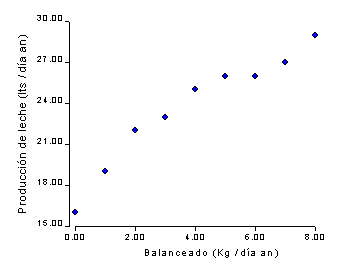
Escriba la ecuación de regresión lineal ajustada e interprete en términos agronómicos los estimadores de los parámetros. Indique en el gráfico el valor de la ordenada al origen.
ŷ = 17,87 + 1,45·x
b₀ = 17,87
Para una dosis de balanceado nula, la producción de leche en un día será de 17,87 litros (no tiene sentido en términos del problema)
b₁ = 1,45
Ante un aumento unitario de dosis de balanceado por día, se obtendrá un aumento en la producción de leche de 1,45.
Según la ecuación propuesta en (a), ¿qué producción de leche promedio puede obtenerse con un nivel de suplemento de 5,5 kg diarios de balanceado por animal?
Si x = 5,5, entonces ŷ = 25.845
Especifique y calcule una medida de error para la estimación realizada en el punto anterior.
Residuo para x = 5,5
e = y observado (del gráfico) - y esperado
e = 25,5 - 25,845 = -0,345
Interprete el valor p < 0,001 de la pendiente en la salida de la matriz de coeficientes de regresión.
La pendiente es significativa para un a del 5 %
H₀: b₁ = 0 vs. H₁: b₁¹ 0.
Autor: Olga Susana Filippini. Argentina.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
- ‹ Anterior |
- Regresar a la guía TP04
- | Siguiente ›
Ejemplo, cómo analizar la regresión lineal