Problema nº 4 de estadística descriptiva, presentar los datos en tablas y distintos tipos gráficos - TP06
Enunciado del ejercicio nº 4
Los siguientes datos representan el número de tomates rechazados por día en un mercado mayorista. Los datos corresponden a 50 días seleccionados aleatoriamente:
| 29 12 83 95 28 | 58 73 23 63 91 | 80 54 71 86 87 | 35 91 63 42 15 | 30 45 47 22 67 | 23 28 87 44 10 | 88 61 36 88 45 | 49 61 8 27 67 | 35 45 94 20 26 | 97 84 26 33 19 |
a) Construya una tabla de frecuencias con 10 clases.
b) Construya un histograma que corresponda a la tabla anterior.
c) Construya un diagrama de caja y bigotes.
d) ¿Qué valor de la variable es superado por el 50 % de las observaciones?
e) ¿Cuál es el valor de la variable que se presenta un mayor número de veces?
f) Utilice todos los datos y la tabla de frecuencias para encontrar la media, el desvío standard y el coeficiente de variación de los números de tomates que se rechazan.
Solución
a)
| Clase | LI | LS | MC | FA | FR | FAA | FRA |
| 1 2 3 4 5 6 7 8 9 10 | 5,00 15,00 25,00 35,00 45,00 55,00 65,00 75,00 85,00 95,00 | 15,00 25,00 35,00 45,00 55,00 65,00 75,00 85,00 95,00 105,00 | 10,00 20,00 30,00 40,00 50,00 60,00 70,00 80,00 90,00 100,00 | 4 5 10 6 3 5 4 3 9 1 | 0,08 0,10 0,20 0,12 0,06 0,10 0,08 0,06 0,18 0,02 | 4 9 19 25 28 33 37 40 49 50 | 0,08 0,18 0,38 0,50 0,56 0,66 0,74 0,80 0,98 1,00 |
Referencias: LI: Límite Inferior de Clase; LS: Límite Superior de Clase; MC: Marca de Clase; FA: Frecuencia Absoluta; FR: Frecuencia Relativa; FAA: Frecuencia Absoluta Acumulada; FRA: Frecuencia Relativa Acumulada.
b)
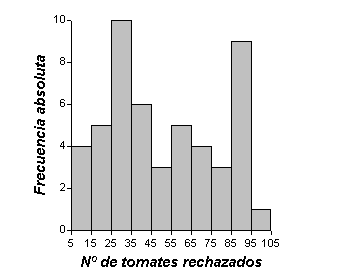
Histograma de frecuencias del número de tomates rechazados por día
c)
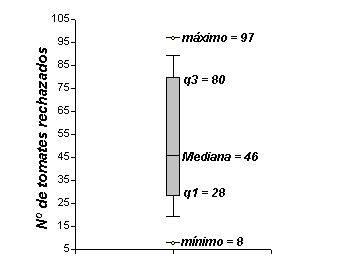
Diagrama de caja del número de tomates rechazados por día
d)
46
e)
45
f)
Datos individuales
| x = | x₁ + x₂ + … + xₙ |
| n |
| x = | 1 | n ∑ i = 1 | xᵢ |
| n |
| x = | 29 + 58 + 80 + … + 29 + 19 |
| 50 |
x = 51,82
| Sₙ² = | 1 | n ∑ i = 1 | (xᵢ - x)² |
| n |
| Sₙ² = | (29 - 51,82)² + … + (19 - 51,82)² |
| 50 |
Sₙ² = 727,75
Sₙ = √727,75 = 26,976
CV = (26,975/51,82)·100 = 52,06 %
| S₍ₙ ₋ ₁₎² = | 1 | n ∑ i = 1 | (xᵢ - x)² |
| n - 1 |
| S₍ₙ ₋ ₁₎² = | (29 - 51,82)² + … + (19 - 51,82)² |
| 49 |
Sₙ² = 742,60
Sₙ = √742,60 = 27,25
CV = (27,25/51,82)·100 = 52,59 %
Datos agrupados
| x = | f₁·m₁ + f₂·m₂ + … + fₖ·mₖ |
| f₁ + f₂ + … + fₖ |
| x = | 1 | k ∑ i = 1 | fᵢ·mᵢ |
| n |
| x = | 10·4 + … + 100·1 |
| 50 |
x = 51,2
| Sₙ² = | 1 | k ∑ i = 1 | fᵢ·(mᵢ - x)² |
| n |
| Sₙ² = | 4·(10 - 51,2)² + … + 1·(100 - 51,2)² |
| 50 |
| Sₙ² = | 37.128 |
| 50 |
Sₙ² = 742,56
Sₙ = √742,56 = 27,25
CV = (27,25/51,2)·100 = 53,22 %
| S₍ₙ ₋ ₁₎² = | 1 | k ∑ i = 1 | fᵢ·(mᵢ - x)² |
| n - 1 |
| S₍ₙ ₋ ₁₎² = | 4·(10 - 51,2)² + … + 1·(100 - 51,2)² |
| 49 |
| S₍ₙ ₋ ₁₎² = | 37.128 |
| 49 |
S₍ₙ ₋ ₁₎² = 757,71
S₍ₙ ₋ ₁₎ = √757,71 = 27,53
CV = (27,53/51,2)·100 = 53,76 %
Autor: Olga Susana Filippini. Argentina.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
- ‹ Anterior |
- Regresar a la guía TP06
- | Siguiente ›
Ejemplo, cómo organizar y presentar los datos en tablas y distintos tipos gráficos