Problema nº 7 de estadística descriptiva ocurrencia de un suceso - TP07

Enunciado del ejercicio nº 7

Sea X una variable aleatoria discreta que sólo toma los valores 0, 1, 2, 3, 4 y 5 y que tiene la distribución de probabilidad dada por la siguiente tabla.

a) Calcule P(2).

b) Calcule μ y σ.

c) Localice el intervalo [μ - 2·σ; μ + 2·σ] sobre el eje X del histograma.

Solución

a)

P(2) = 1 - 0,05 - 0,30 - 0,20 - 0,10 - 0,05

P(2) = 0,30

b)

μ = 0·0,05 + 1·0,30 + 2·0,30 + 3·0,20 + 4·0,10 + 5·0,05

μ = 2,15

σ² = 0,05·(0 - 2,15)² + 0,30·(1 - 2,15)² + 0,20·(2 - 2,15)² + … + 0,05·(5 - 2,15)² = 1,5275

σ = (σ²)^½

σ = √1,5275

σ = 1,2359

c)

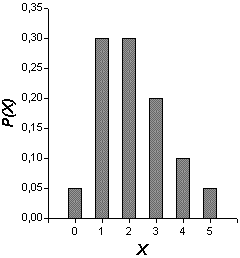
[μ - 2·σ; μ + 2·σ] = [2,15 - 2·1,2359; 2,15 + 2·1,2359] = [-0,3218; +4,6218].

Autor: Olga Susana Filippini. Argentina.

Editor: Ricardo Santiago Netto (Administrador de Fisicanet).

• ‹ Anterior |
• Regresar a la guía TP07
• | Siguiente ›

Ejemplo, cómo calcular la probabilidad de que ocurra un suceso