Problema nº 4 de casos de factoreo o factorización, factorizar paso a paso - TP08
Enunciado del ejercicio nº 4
Efectuar las siguientes operaciones de factorización (paso a paso):
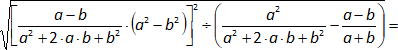
Solución
Los denominadores "a² + 2·a·b + b²" son trinomio cuadrado perfecto, los factorizamos:
a² + 2·a·b + b² = (a + b)²
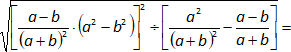
El producto "a² - b²" es una diferencia de cuadrados:
a² - b² = (a - b)·(a + b)
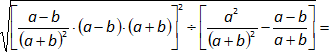
Simplificamos:
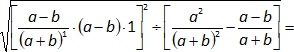
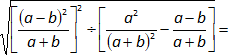
Sumamos las fracciones, el denominador común es "(a + b)²":
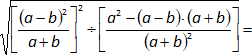
El producto (a - b)·(a + b) es una diferencia de cuadrados:
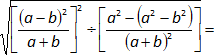
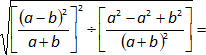
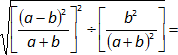
Expresamos la división como un producto:
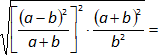
Aplicamos distributiva de la potencia con respecto a la división:
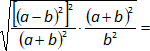
Simplificamos:
![]()
Resolvemos la raíz y expresamos el resultado:
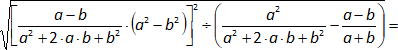
| = | (a - b)² |
| b |
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP08
- | Siguiente ›
Ejemplo, cómo factorizar paso a paso