Ejemplo, cómo resolver y graficar sistemas de ecuaciones lineales

Problema n° 3 de funciones lineales - TP01

Enunciado del ejercicio n° 3

Hallar el punto de intersección y graficar:

r: x + y + 1 = 0

r': x - y + 1 = 0

Para hallar el punto de intersección de las rectas debemos resolver el sistema. En este caso sumamos ambas ecuaciones:

2·x + 2 = 0

Despejamos "x":

2·x = -2

x = -2/2

x = -1

Con el valor de "x" reemplazamos en cualquiera de las ecuaciones y hallaremos "y":

r: x + y + 1 = 0

-1 + y + 1 = 0

y = 0

El punto de intersección es:

P(-1; 0)

Para graficar las rectas las expresamos en forma explícita:

r: y = -x - 1

r': y = x + 1

De esta forma las pendientes y las ordenadas al origen son:

m₁ = -1

b₁ = -1

m₂ = 1

b₂ = 1

Graficamos:

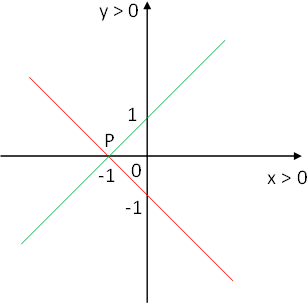
Gráfica de rectas perpendiculares

Autor: Ricardo Santiago Netto (Administrador de Fisicanet)

San Martín. Buenos Aires. Argentina.