Superficies en ℜ³

Gráficas típicas de las superficies en el espacio (ℜ³) según las ecuaciones características y haciendo variar los coeficientes.

M·x² + N·y² + P·z² = R

Gráficas de las superficies en en R³ según los valores adoptados de M, N, P y R

M, N, P	Lugar geométrico obtenido
Con R > 0
Todos positivos	Elipsoide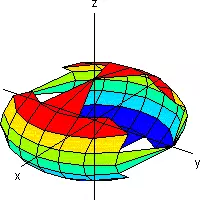
Todos positivos e iguales	Esfera
Todos negativos	No existe lugar geométrico
2 positivos y uno negativo	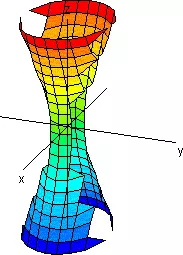Hiperboloide de una hoja
2 negativos y uno positivo	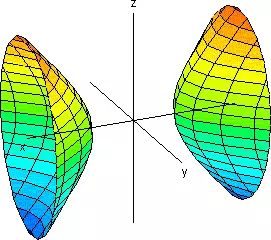Hiperboloide de dos hojas
1 cero y dos positivos	Cilindro Elíptico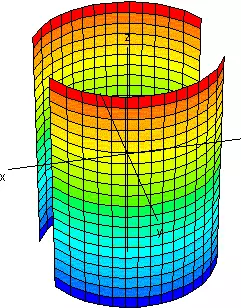
1 cero y dos positivos iguales	Cilindro Circular
1 cero y 2 negativos	No existe lugar geométrico
1 cero, 1 positivo y 1 negativo	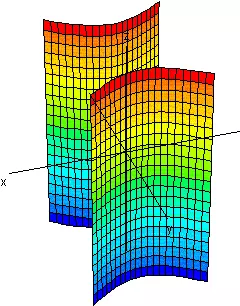Cilindro Hiperbólico
2 ceros y 1 positivo	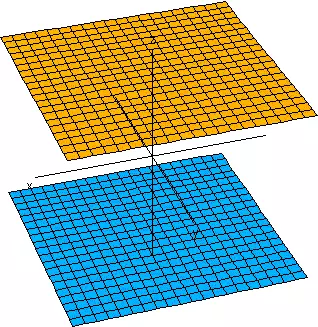Dos planos paralelos
2 ceros y 1 negativo	No existe lugar geométrico

M·x² + N·y² + P·z² = R

Gráficas de las superficies en en R³ según los valores adoptados de M, N, P y R

M, N, P	Lugar geométrico obtenido
Con R = 0
Todos del mismo signo	Un punto P(0, 0, 0)
2 positivos y 1 negativo	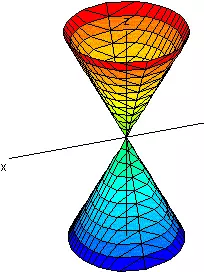Cono recto
1 cero y 2 del mismo signo	Eje coordenado
1 cero y 2 de distinto signo	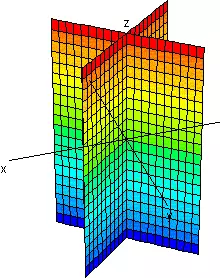Dos planos que se cortan
2 cero	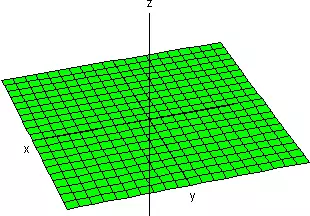Plano coordenado

M·x² + N·y² = S·R

Gráficas de las superficies en en R³ según los valores adoptados de M, N, P y R

M y N	Lugar geométrico Obtenido
Con S > 0
Del mismo signo	Paraboloide Elíptico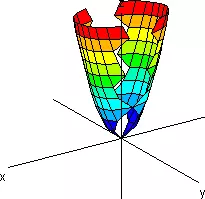
Del mismo signo iguales	Paraboloide Circular
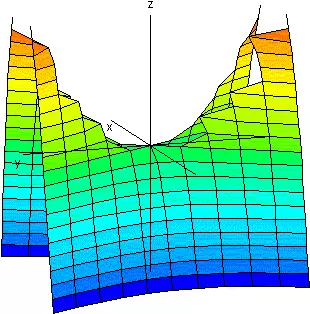
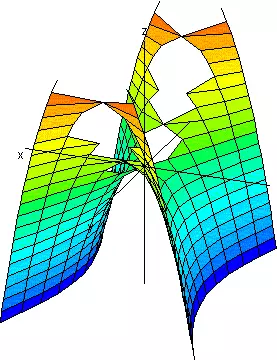
Signos Opuestos	Paraboloide Hiperbólico
Uno es Cero	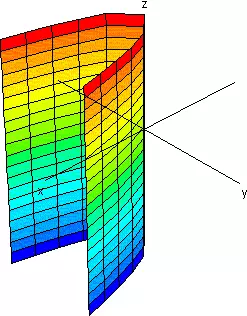Cilindro Parabólico
Con S = 0
Uno es Cero	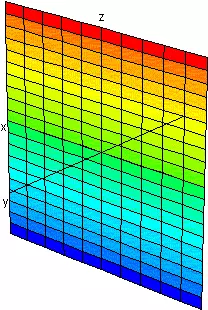Plano Coordenado
Del mismo signo	Eje Coordenado
Signos Opuestos	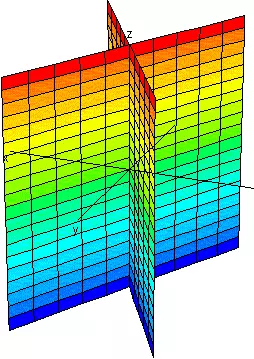Planos que se cortan

Editor: Ricardo Santiago Netto (Administrador de Fisicanet).