Problema nº 9 de funciones de varias variables, longitud de una curva aplicando integrales - TP01
Enunciado del ejercicio nº 9
Calcular la longitud de la curva y = log (cos x); 0 ≤ x ≤ π/4
Desarrollo
Fórmulas:
![]()
![]()
Solución
f(x) = log (cos x)
f'(x) = -sen x/cos x
Planteamos la integral correspondiente entre los límites indicados:
![]()
| s = ∫ | π/4 | √1 + (-sen x/cos x)²·dx |
| 0 |
Trabajando con la integranda:
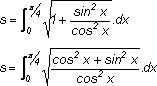
| s = ∫ | π/4 | √1/cos² x·dx |
| 0 |
| s = ∫ | π/4 | 1/cos x·dx |
| 0 |
Integrando:
| s = log ( | cos x | ) | π/4 |
| 1 - sen x | |||
| 0 |
| s = log ( | cos π/4 | - | cos 0 | ) |
| 1 - sen π/4 | 1 - sen 0 |
| s = log ( | √2 | - | ) | |||
| 2 | 1 | |||||
| 1 - | √2 | 1 - 0 | ||||
| 2 |
| s = log | √2 | - log 1 |
| 2 | ||
| 2 - √2 | ||
| 2 |
| s = log | √2 |
| 2 - √2 |
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP01
- | Siguiente ›
Ejemplo, cómo hallar la longitud de una curva aplicando integrales