Problema nº 25 de funciones de varias variables, longitud de una curva aplicando integrales - TP02
Enunciado del ejercicio nº 25
Calcular el perímetro del dominio plano:
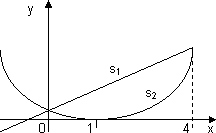
Gráfico del perímetro de un dominio plano
(x - 1)² ≤ 4·y ≤ 1 + 2·x
Desarrollo
Fórmulas:
| s = ∫ | t₂ | ||X'(t)||·dt |
| t₁ |
| s = ∫ | b | √1 + [f'(x)]²·dx |
| a |
Solución
Para el perímetro calculamos la longitud de ambas curvas y luego las sumamos.
s₁ ⇒ y = ½·x + ¼ ⇒ y' = ½
s₂ ⇒ y = ¼·(x - 1)²
y' = ½·(x - 1)
s = s₁ + s₂
Hallamos los límites de integración:
(x - 1)² = 1 + 2·x
x² - 2·x + 1 = 1 + 2·x
x² - 4·x = 0
x·(x - 4) = 0
x₁ = 0 y x₂ = 4
Planteamos las integrales:
| s₁ = ∫ | 4 | √1 + (½)²·dx |
| 0 |
| s₂ = ∫ | 4 | √1 + [½·(x - 1)]²·dx |
| 0 |
Resolvemos:
| s₁ = ∫ | 4 | √1 + ¼·dx |
| 0 |
| s₁ = √5/4·∫ | 4 | dx |
| 0 |
| s₁ = ½·√5·x | 4 |
| 0 |
s₁ = ½·√5·4 - ½·√5·0
s₁ = 2·√5
Para la segunda integral aplicamos un cambio de variable:
½·(x - 1) = sinh t
dx = 2·cosh t
s₂ = 2·∫ √1 + sinh² t·cosh t·dt
Como:
cosh t = √1 + sinh² t
s₂ = 2·∫ cosh t·cosh t·dt
s₂ = 2·∫ cosh² t·dt
s₂ = 2·[½·(t + sinh t·cosh t)]
s₂ = t + sinh t·cosh t
Revirtiendo el cambio de variable con:
t + sinh t·cosh t = log {½·(x - 1) + √1 + [½·(x - 1)]²} + ½·(x - 1)·√1 + [½·(x - 1)]²
| s₂ = log {½·(x - 1) + √1 + [½·(x - 1)]²} + ½·(x - 1)·√1 + [½·(x - 1)]² | 4 |
| 0 |
s₂ = [log {½·(4 - 1) + √1 + [½·(4 - 1)]²} + ½·(4 - 1)·√1 + [½·(4 - 1)]²] - [log {½·(0 - 1) + √1 + [½·(0 - 1)]²} + ½·(0 - 1)·√1 + [½·(0 - 1)]²]
s₂ = {log [½·3 + √1 + (½·3)²] + ½·3·√1 + (½·3)²} - [log {½·(-1) + √1 + [½·(-1)]²} + ½·(-1)·√1 + [½·(-1)]²]
s₂ = [log (3/2 + √1 + 9/4) + (3/2)·√1 + 9/4] - [log (-½ + √1 + ¼) - ½·√1 + ¼]
s₂ = [log (3/2 + √13/4) + (3/2)·√13/4] - [log (-½ + √5/4) - ½·√5/4]
| s₂ = log ( | 3 | + | 1 | ·√13) + | 3 | · | 1 | ·√13 - log ( | -1 | + | 1 | ·√5) + | 1 | · | 1 | ·√5 |
| 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| s₂ = log | 3 + √13 | + | 3 | ·√13 - log | √5 - 1 | + | 1 | √5 |
| 2 | 4 | 2 | 4 |
| s₂ = log | ½·(3 + √13) | + | 3 | ·√13 + | 1 | √5 |
| ½·(√5 - 1) | 4 | 4 |
| s₂ = log | 3 + √13 | + | 3 | ·√13 + | 1 | √5 |
| √5 - 1 | 4 | 4 |
Sumando:
| s = 2·√5 + log | 3 + √13 | + | 3 | ·√13 + | 1 | √5 |
| √5 - 1 | 4 | 4 |
| s = log | 3 + √13 | + | 3 | ·√13 + | 9 | √5 |
| √5 - 1 | 4 | 4 |
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP02
- | Siguiente ›
Ejemplo, cómo hallar la longitud de una curva aplicando integrales