Figuras del espacio. Geometría
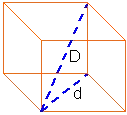
Cubo
D … diagonal del cubo
d … diagonal de una cara
a … arista del cubo
d = a·√2
D = a·√3
Ab = a²
SL = 4·a²
ST = 6·a²
V = a³
√2 = 1,41
√3 = 1,73
V en m³ ⟶ Cap = V·1.000
V en dm³ ⟶ Cap = V
V en cm³ ⟶ Cap = V/1.000
Pbtriángulo equilátero = l·3
Abtriángulo equilátero = l²·√3/4
Pbcuadrado = l·4
Abcuadrado = l²
Pbhexágono = l·6
Abhexágono = 3·l²·√3/2
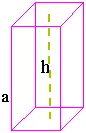
Prisma
Pb = depende del polígono de la base
Ab = depende del polígono de la base
SL = Pb·h
ST = SL + 2·Ab
V = Ab·h
arista lateral = h
Cilindro
Pb = Cia = 2·π·R
Ab = Co = π·R²
SL = Pb·h
ST = SL + 2·Ab
V = Ab·h
generatríz = h
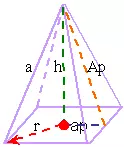
Pirámide
h … altura de la pirámide
Ap … apotema de la pirámide
a … arista lateral de la pirámide
ap … apotema de la base
r … radio de la base
Pb = depende del polígono de la base
Ab = depende del polígono de la base
SL = Pb·Ap/2
ST = SL + Ab
V = Ab·h/3
Ap² = h² + ap²
a² = h² + r²
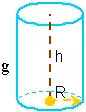
Cono
g … generatríz del cono
h … altura del cono
R … radio de la base
Pb = Cia = 2·π·R
Ab = Co = π·R²
SL = Pb·g/2
ST = SL + Ab
V = Ab·h/3
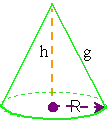
g² = h² + ℜ²
Esfera
d … distancia entre las circunferencias
R … radio de la circunferencia máxima o de la esfera
r … radio de cualquier circunferencia menor
π = 3,14
Ciaₘₐₓ = 2·π·R
Ciamenor = 2·π·r
Coₘₐₓ = π·R²
Comenor = π·r²
A = 4·π·R²
V = 4·π·R³/3
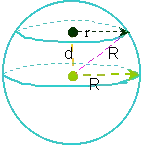
R² = r² + d²
aptriángulo equilátero = l·√3/6
rtriángulo equilátero = l/√3
apcuadrado = l/2
rcuadrado = l/√2
aphexágono = l·√3/2
rhexágono = l
Autor: Hugo David Giménez Ayala. Paraguay.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
Fórmulas y elementos para resolver figuras en el espacio