Guía nº 1 de ejercicios de geometría

Resolver los siguientes ejercicios

Problema nº 1

Dados tres puntos, A, B y C, no alineados, dibujar: La semirrecta de origen C que contiene al punto B, y la AB'.

Problema nº 2

Dibujar dos semirrectas que tengan el mismo origen y no sean opuestas.

Problema nº 3

¿Qué figura constituye la unión del conjunto de los puntos de la AB' y los de la semirrecta de origen A que no contiene al punto B?

Problema nº 4

Dibujar, sobre una recta, cuatro segmentos consecutivos.

Problema nº 5

¿Cuál es la figura formada por la intersección del conjunto de puntos de la semirrecta de origen A que contiene al punto B y de la semirrecta de origen B que no contiene al punto A?

Problema nº 6

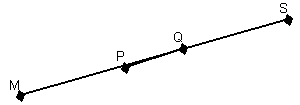
Dados los puntos M, P, Q y S de la figura, hallar:

PS' ∩ QS'
MQ' ∩ QP'
MQ' ∩ PS'
MQ' ∪ PS
MQ ∪ PS

Problema nº 7

Decir cual es el conjunto de los puntos tal que su intersección con XY de por resultado el XY.

Problema nº 8

Comprobar, en un ejemplo, el carácter transitivo de la relación de mayor entre segmentos.

Problema nº 9

Comprobar, en un ejemplo, el carácter transitivo de la relación de menor entre segmentos.

Problema nº 10

¿Si AB = CD y CD < EF, cómo es EF con respecto a AB?

Problema nº 11

¿Si AB > MN y MN = EF, cómo es EF con respecto a AB?

Problema nº 12

¿Si AB > CD, CD = EF y EF no es mayor que MN, cómo es AB con respecto a MN?

Problema nº 13

¿Si MN = PQ, PQ > RS y RS no es menor que TV, cómo es MN con respecto a TV?

Problema nº 14

Verificar gráficamente en una suma de tres segmentos, la propiedad conmutativa.

Problema nº 15

Verificar gráficamente en una suma de cinco segmentos, la propiedad asociativa.

Problema nº 16

¿Si AB > CD y MN > PQ, cómo es AB + MN con respecto a CD + PQ?

Problema nº 17

¿Si RS < CD y AB = MN, cómo es RS + MN con respecto a AB + CD?

Problema nº 18

¿Si AB < MN, cómo es AB × 6 con respecto a MN × 6?

Problema nº 19

¿Si AB + CD + EF = MN, cómo es MN con respecto a AB?

Problema nº 20

Comprobar gráficamente las propiedades de la resta de segmentos.

Problema nº 21

Expresar en símbolos las propiedades de la resta de segmentos.

Problema nº 22

Dibujar un segmento y hallar su duplo, su triplo y su cuádruplo.

Problema nº 23

Si un segmento se divide por tres y a ese resultado se lo multiplica también por tres, ¿qué segmento se obtiene? Comprobarlo gráficamente.

Problema nº 24

Dibujar un segmento, y mediante un hilo dividirlo aproximadamente en dos, tres, cuatro, y seis partes iguales.

Autor: Ricardo Santiago Netto. Argentina