Integrales triples (segunda parte)
Teoremas
Teorema de Gauss (o de la divergencia)
Observación:
Con éste método se calcula el vector normal exterior a la superficie.
∯S F·ds = ∭V ∇F·dx·dy·dz
∇F: Divergencia.
Te dan el flujo de una determinada función F(x, y, z). Delimitan una superficie con planos o superficies y piden calcular el flujo a través de la superficie frontera.
Divergencia:
| ∇F = | ∂F₁ | + | ∂F₂ | + | ∂F₃ | (*) |
| ∂x | ∂y | ∂z |
(*) derivadas de las componentes de la función del flujo.
Observación:
Si me queda el flujo neto negativo, significa que tiene sentido opuesto al normal exterior.
Puntos: Fuente: origina campo (campo positivo). Sumidero: recibe campo. Pasante: Lo que entra es igual a lo que sale.
Teorema de Stocks (o del rotor)
∮C F·dl = ∬S ∇×F·ds
Observación:
La relación entre la orientación de la curva y de la superficie esta dada por la regla de la mano derecha.
En práctica: Te piden calcular la circulación de una F(x, y, z) a lo largo de una curva.
| ∇×F = | i | j | k |
| ∂/∂x | ∂/∂y | ∂/∂z | |
| F₁ | F₂ | F₃ |
(F₁, F₂, F₃) Componentes del campo que circula.
Componente i = (∂/∂y)·F₃ - (∂/∂z)·F₂ (derivada respecto de y de F₃ menos la derivada respecto de z de F₂)
∮C F·dl = ∬Axy ∇×F ∇F / |F'z|
El gradiente del plano en el que encuentro la figura.
El gradiente me define un sentido de recorrido con la regla de la mano derecha. Cuando recorro la figura debo respetar este sentido.
| Es distinto ∫ | π | que ∫ | 0 | . |
| 0 | π |
Teorema de Green
Teorema de Stokes aplicado al plano XY:
| ∮C+ F·dl = ∬S ( | ∂F₂ | - | ∂F₁ | )·dx·dy |
| ∂x | ∂y |
Observación:
El sentido de circulación corresponde a recorrer la curva de manera tal que la región S queda a la izquierda (en general sentido antihorario).
Observación:
Verificar que el campo F y sus derivadas están definidos en toda la región S.
Aplicación al cálculo de áreas:
| ∮C+ F·dl = ∬S ( | ∂F₂ | - | ∂F₁ | )·dx·dy |
| ∂x | ∂y |
Si:
| Si ( | ∂F₂ | - | ∂F₁ | ) es una constante K: |
| ∂x | ∂y |
∮C+ F·dl = ∬SK·dx·dy (con K ≠ 0) = K Área (S)
Área (S) = 1/K ∮C+ F·dl,
| con ( | ∂F₂ | - | ∂F₁ | ) = K ≠ 0 |
| ∂x | ∂y |
Caso particular:
| F(x, y) = (0, x) ⇒ | ∂F₂ | - | ∂F₁ | = 1 |
| ∂x | ∂y |
Luego:
Área (S) = ∮C+ (0, x)·dl
Ejemplo nº 3
Cálculo del área de la elipse:
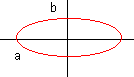
Gráfico para calcular el área de la elipse
| x² | + | y² | = 1 |
| a² | b² |
G(θ) = (a·cos θ, b·sen θ)
Área (S) = ∮C+ (0, x)·dl
| S = ∫ | 2·π | (0, a·cos θ)·a·(-sen θ, b·cos θ)·dθ |
| 0 |
| S = ∫ | 2·π | a·b·cos² θ·dθ |
| 0 |
| S = a·b·(½·θ + sen ¼·2·θ) | 2·π |
| 0 |
Por tabla:
S = a·b·(π + 0)
S = a·b·π
Campos conservativos
∃ φ/ F(x) = ∇ φ(x)
Condición necesaria: Derivadas cruzadas iguales.
Búsqueda de φ:
F = (f₁, f₂) = (φ' x, φ' y)
φ = ∫ φ'x·dx = ∫ f₁·dx = f₁(x, y) + k(y)
φ = ∫ φ'y·dy = ∫ f₂·dy = f₂(x, y) + δ(x)
Luego, se construye con los términos comunes colocados 1 sola vez más los términos no comunes más una constante pura
Integral por sustitución
u = 4 - r²
Nuevos límites de interacción: reemplaza por 2 y 0 en u = 4 - r²
4 - 2² = 0 ⟶ 0 (superior)
4 - 0² = 4 ⟶ (inferior)
du = -2·r·dr
-½·du = r·dr
| ∫ | 2 | r·√(4 - r²)·dr = ∫ | 0 | √ŭ·(-½·du) = |
| 0 | 4 |
| = ½·∫ | 4 | √ŭ·du = ½·½· | 1 √ŭ | 4 | = |
| 0 | 0 |
= ½·½·¼ = 1/16
Para el cálculo de Volúmenes y áreas se puede verificar con fórmulas ya conocidas:
Volumen esfera = (4/3)·π·ℜ³
Área elipse = a·b·π
Luego, sumando y restando estos valores conocidos, se puede verificar el resultado.
Ecuaciones diferenciales
Orden: el número de la derivada más alta.
Grado: el exponente de la derivada más alta
(Y')² + Y = 4 (primer orden segundo grado)
Ecuación de primer orden:
y' + a(x) y = b(x) lineales
Identifico a(x) y b(x). Si y' tiene un coeficiente se lo debe sacar multiplicando a ambos miembros por 1/ constante (esta constante puede ser una x).
Cálculo u(x):
u(x) = e∫ a(x)·dx
Y
| g(x) = | ∫ u(x)·b(x)·dx + c |
| u(x) |
y averiguo la solución general. Calculo c para el problema en particular con algún punto dato que nos hayan dado.
Regla de la mano derecha:
Demostraciones que se piden para los finales
Si existe la derivada direccional en un punto, existen las derivadas de las componentes y viceversa:
∃ F'(x₀, ř) ⇔ ∃ F i' (x₀, ř), 1 ≤ i ≤ m
| F'(x₀, ř) = | lim h ⟶ 0 | F(x₀ + h·ř) - F(x₀) | = | lim h ⟶ 0 | G(h) |
| h |
| ∃ | lim h ⟶ 0 | G(h) ⇔ ∃ = | lim h ⟶ 0 | Gᵢ(h) |
1 ≤ i ≤ m
| lim h ⟶ 0 | Gᵢ(h) = | lim h ⟶ 0 | Fᵢ(x + h·ř) - Fᵢ(x₀) |
| h |
| lim h ⟶ 0 | Gᵢ(h) = Fᵢ' (x₀ + h·ř) |
1 ≤ i ≤ m
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
- ‹ Anterior
- |
- Siguiente ›