Integrales triples (primera parte)
Cálculo de volúmenes
Vol (v) = ∭V dx·dy·dz
Cálculo de masas
Masa (M) = ∭V δ(x, y, z)·dx·dy·dz
Centro de masa
| ∭V x·δ(x, y, z)·dx·dy·dz |
| M |
Momento de inercia
I₀ = ∭V d²·δ(x, y, z)·dx·dy·dz
Extensión del teorema de Fubini a regiones generales:
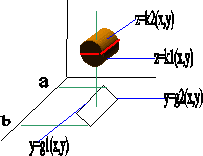
| ∭V F(x, y, z)·dx·dy·dz = ∫ | b | ∫ | g2 | ∫ | k2 | F(x, y, z)·dx·dy·dz |
| a | g1 | k1 |
Teorema:
Cambio de variables:
Dada f:k ⊂ ℜ³ ⟶ ℜ, F contínua, G: r* ⊂ ℜ³ ⟶ ℜ³, G ∈ C¹, inyectiva con G(k*), tal que det (DG (u, v, w) ≠ 0, ∀ (u, v, w) ∈ k*): entonces:
∭ₖ F(x, y, z)·dx·dy·dz = ∭ₖ F(g(u, v, w))·|det (DG)|·du·dv·dw
F(x, y, z) = dv
F(g(x, y, z))·|det (DG)| = dv
Observación:
El teorema sigue siendo válido si det DG(u, v, w) = 0 sobre un conjunto de puntos de medida 0 en k*.
Aplicación: Coordenadas cilíndricas:
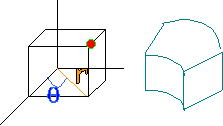
Gráfico de interpretación de las coordenadas cilíndricas
X = r·cos θ
Y = r·sen θ
Z = z
r = √(x² + y²) (distancia al eje Z)
G(r·cos θ, r·sen θ, z)
∭ₖ F(x, y, z)·dx·dy·dz = ∭k* F(r·cos θ, r·sen θ, z)·r·dz·dr·dθ
Método de trabajo:
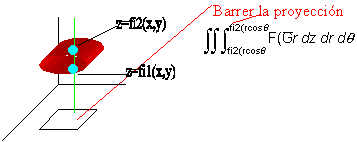
Ejemplo nº 1
Calcular el volumen de μ limitado por √(x² + y²) ≤ z ≤ R
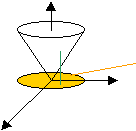
Gráfico para el cálculo del volumen
| Volumen = ∫ | 2·π | ∫ | R | ∫ | R | r·dz·dr·dθ |
| 0 | 0 | r |
| Volumen = ∫ | 2·π | ∫ | R | (R·r - r²)·dr·dθ |
| 0 | 0 |
| Volumen = ∫ | 2·π | (R·½·r² - ⅓·r³) | R | dθ |
| 0 | 0 |
| Volumen = ∫ | 2·π | (R·½·R² - ⅓·R³)·dθ |
| 0 |
| Volumen = ∫ | 2·π | (½·R³ - ⅓·R³)·dθ |
| 0 |
| Volumen = ⅙·R³·∫ | 2·π | dθ |
| 0 |
Volumen = ⅓·π·R³
Integrales de superficie:
En superficie (reemplazar Z por su valor en la superficie).
| Área (s) = ∬Axy | |∇F| | ·dx·dy |
| |F'z| |
| Flujo (Φ) = ∬Axy | F·∇F | ·dx·dy |
| |F'z| |
Ejemplo nº 2
s:z = √(x² + y²)
Límites: x² + y² ≤ R
Gráfico para el cálculo de la superficie
F(x, y, z) = √(x² + y²) -z
| F'x = | x |
| √(x² + y²) |
| F'y = | y |
| √(x² + y²) |
F'z = -1
| ∇F = ( | x | , | y | , -1) |
| √(x² + y²) | √(x² + y²) |
|∇F| = √2
| Área = ∬Axy | |∇F| | ·dx·dy |
| |F'z| |
| Área = ∬Axy | √2 | ·dx·dy |
| |-1| |
Área = ∬Axy √2·dx·dy
Área = √2·∬Axy dx·dy
Área = √2·π·R²
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
- ‹ Anterior
- |
- Siguiente ›