Problema nº 6 de integrales, cálculo del momento de inercia de sólidos - TP08
Enunciado del ejercicio nº 6
Calcular el momento de inercia, respecto del eje z, del siguiente sólido homogéneo
{(x, y, z): x² + y² + z² ≤ 2, x² + y² - z² ≤ 0, z ≥ 0}
Desarrollo
Fórmulas:
Para sólidos homogéneos:
Iz = ∭D (x² + y²) dx·dy·dz
Solución
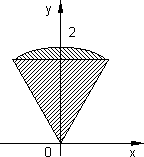
Gráfico del dominio para el cálculo del momento de inercia
Calculamos el volumen:
V = ∭D dx·dy·dz
Cambiamos a coordenadas polares:
V = ∭D dx·dy·dz = ∭D' r²·sen φ·dθ·dφ·dr
0 ≤ θ ≤ 2·π
0 ≤ φ ≤ π/4
0 ≤ r ≤ √2
V = ∭D dx·dy·dz
| V = ∫ | 2·π | dθ∫ | π/4 | sen φ·dφ∫ | √2 | r²·dr |
| 0 | 0 | 0 |
Como las variables no dependen entre si:
| V = (θ) | 2·π | ·(-cos φ) | π/4 | ·(⅓·r³) | √2 | = |
| 0 | 0 | 0 |
V = (2·π - 0)·(-cos π/4 + cos 0)·[⅓·(√2)³ - ⅓·0³]
V = 2·π·(-cos π/4 + cos 0)·⅓·(√2)³
V = 2·π·(-½·√2 + 1)·⅔·√2
V = 2·π·½·(2 - √2)·⅔·√2
V = (2 - √2)·⅔·π·√2
Luego mediante un cambio de coordenadas:
| x = r·(cos θ)·(sen φ) y = r·(sen θ)·(sen φ) z = r·cos φ | ⟶ |J| = r²·sen φ |
∭D (x² + y²)·dx·dy·dz = ∭D' [(r·(cos θ)·(sen φ))² + (r·(sen θ)·(sen φ))²]·r²·sen φ·dθ·dφ·dr =
= ∭D' (r²·(cos² θ)·sen² φ) + r²·(sen² θ)·(sen² φ)·r²·(sen φ)·dθ·dφ·dr = ∭D' r²·(sen² φ)·(cos² θ + sen² θ)·r²·sen φ·dθ·dφ·dr =
= ∭D' r⁴·(sen³ φ)·dθ·dφ·dr =
| = ∫ | 2·π | dθ∫ | π/4 | sen³ φ·dφ∫ | √2 | r⁴·dr = |
| 0 | 0 | 0 |
| = (θ) | 2·π | ·(⅕·r⁵) | √2 | ·∫ | π/4 | (1 - cos² φ)·sen φ·dφ = |
| 0 | 0 | 0 |
| = 2·π·⅕·(√2)⁵·∫ | π/4 | (sen φ - sen φ·cos² φ)·dφ = |
| 0 |
| = 2·π·⅕·4·√2·[∫ | π/4 | (sen φ - sen φ·cos² φ)·dφ] = |
| 0 |
| = ⅕·8·π·√2·[∫ | π/4 | sen φ·dφ + ∫ | π/4 | cos² φ·d(cos φ)] = |
| 0 | 0 |
| = ⅕·8·π·√2·[(-cos φ) | π/4 | + (⅓·cos³ φ) | π/4 | ] = |
| 0 | 0 |
= ⅕·8·π·√2·[(-cos π/4 + cos 0) + (⅓·cos³ π/4 - ⅓·cos³ 0) =
| = | 8·π·√2 | ·[- | √2 | + 1 + | (½·√2)³ | - | 1 | ] = |
| 5 | 2 | 3 | 3 |
| = | 8·π·√2 | ·[- | √2 | + 1 + | √2 | - | 1 | ] = |
| 5 | 2 | 12 | 3 |
| = | 8·π·√2 | ·( | -6·√2 + 12 + √2 - 4 | ) = |
| 5 | 12 |
| = | 8·π·√2 | ·( | -5·√2 + 8 | ) = |
| 5 | 12 |
| = | 2·π·√2 | ·(8 - 5·√2) |
| 15 |
Finalmente:
Iz = (M/V)·∭D (x² + y²)·dx·dy·dz
| Iz = | M | · | 2·π·√2 | ·(8 - 5·√2) |
| (2 - √2)·⅔·π·√2 | 15 |
Resultado, el momento de inercia del sólido es:
| Iz = | M·(8 - 5·√2) |
| 5·(2 - √2) |
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP08
- | Siguiente ›