Problema n° 7 de integrales
Enunciado del ejercicio n° 7
Calcular el momento de inercia, respecto del eje z, del siguiente sólido homogéneo
{(x, y, z): x² + y² ≤ z², (x - 1)² + y² ≤ 1, 0 ≤ z ≤ 4}
Desarrollo
Fórmulas:
Para sólidos homogéneos:
Iz = ∭D (x² + y²) dx·dy·dz
Solución
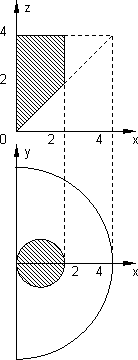
Gráfico del dominio para el cálculo del momento de inercia
Calculamos el volumen:
V = ∭D dx·dy·dz
| V = ∬Dxy dx·dy∫ | 4 | dz |
| √x² + y² |
| V = ∬Dxy [z] | 4 | dx·dy |
| √x² + y² |
V = ∬Dxy (4 - √x² + y²)·dx·dy
Cambiando a coordenadas polares:
| x = r·cos θ y = r·sen θ | → |J| = r |
V = ∬D'xy [4 - √(r·cos θ)² + (r·sen θ)²]·r·dθ·dr
V = ∬D'xy (4 - √r²·cos² θ + r²·sen² θ)·r·dθ·dr
V = ∬D'xy [4 - √r²·(cos² θ + sen² θ)]·r·dθ·dr
V = ∬D'xy (4 - √r²)·r·dθ·dr
V = ∬D'xy (4·r - r²)·dθ·dr
Hallamos el límite de integración correspondiente a r:
(x - 1)² + y² = 1
(r·cos θ - 1)² + (r·sen θ)² = 1
r²·cos² θ - 2·r·cos θ + 1 + r²·sen² θ = 1
r²·(cos² θ + sen² θ) - 2·r·cos θ = 0
r² - 2·r·cos θ = 0
r·(r - 2·cos θ) = 0
0 ≤ r ≤ 2·cos θ
Para θ:
-π/2 ≤ θ ≤ π/2
| V = ∫ | π/2 | dθ∫ | 2·cos θ | (4·r - r²)·dr |
| -π/2 | 0 |
| V = 2·∫ | π/2 | [4·½·r² - ⅓·r³] | 2·cos θ | dθ |
| 0 | 0 |
| V = 2·∫ | π/2 | [2·(2·cos θ)² - ⅓·(2·cos θ)³]·dθ |
| 0 |
| V = 2·∫ | π/2 | (2·4·cos² θ - ⅓·8·cos³ θ)·dθ |
| 0 |
| V = 2·∫ | π/2 | (8·cos² θ - ⅓·8·cos³ θ)·dθ |
| 0 |
| V = 16·∫ | π/2 | (cos² θ - ⅓·cos³ θ)·dθ |
| 0 |
cos³ θ = cos θ·(1 - sen² θ) = cos θ - cos θ·sen² θ
| V = 16·∫ | π/2 | [cos² θ - ⅓·(cos θ - cos θ·sen² θ)]·dθ |
| 0 |
| V = 16·∫ | π/2 | (cos² θ - ⅓·cos θ - ⅓·cos θ·sen² θ)·dθ |
| 0 |
| V = 16·[½·θ + ½·sen θ·cos θ - ⅓·sen θ - ⅓·⅓·sen³ θ] | π/2 |
| 0 |
V = 16·(½·π/2 + ½·sen π/2·cos π/2 - ⅓·sen π/2 - ⅑·sen³ π/2) - 16·(½·0 + ½·sen 0·cos 0 - ⅓·sen 0 - ⅑·sen³ 0)
V = 16·(¼·π + ½·1·0 - ⅓·1 - ⅑·1) - 16·(0 + ½·0·1 - ⅓·0 - ⅑·0)
V = 16·(¼·π - ⅓ - ⅑)
V = 16·(¼·π - 4/9)
V = 4·π - 16·(4/9)
V = 4·π - 64/9
Ahora calculamos la integral:
Iz = ∭D (x² + y²)·dx·dy·dz
| Iz = | M V | ·∭Dxy (x² + y²)·dx·dy∫ | 4 | ·dz |
| √x² + y² |
| Iz = | M V | ·∭Dxy [z] | 4 | (x² + y²)·dx·dy |
| √x² + y² |
| Iz = | M V | ·∭Dxy (4 - √x² + y²)·(x² + y²)·dx·dy |
Cambiando a coordenadas polares:
| x = r·cos θ y = r·sen θ | → |J| = r |
| Iz = | M V | ·∭D'xy [4 - √(r·cos θ)² + (r·sen θ)²]·[(r·cos θ)² + (r·sen θ)²]·r·dθ·dr |
| Iz = | M V | ·∭D'xy (4 - √r²·cos² θ + r²·sen² θ)·(r²·cos² θ + r²·sen² θ)·r·dθ·dr |
| Iz = | M V | ·∭D'xy [4 - √r²·(cos² θ + sen² θ)]·r²·(cos² θ + sen² θ)·r·dθ·dr |
| Iz = | M V | ·∭D'xy (4 - √r²·1)·r³·1·dθ·dr |
| Iz = | M V | ·∭D'xy (4 - √r²)·r³·dθ·dr |
| Iz = | M V | ·∭D'xy (4 - r)·r³·dθ·dr |
| Iz = | M V | ·∭D'xy (4·r³ - r4)·dθ·dr |
Los límites de integración son los mismos:
0 ≤ r ≤ 2·cos θ
-π/2 ≤ r ≤ π/2
| Iz = | M V | ∫ | π/2 | dθ∫ | 2·cos θ | (4·r³ - r4)·dr |
| -π/2 | 0 |
| Iz = | 2·M V | ∫ | π/2 | dθ∫ | 2·cos θ | (4·r³ - r4)·dr |
| 0 | 0 |
| Iz = | 2·M V | ∫ | π/2 | [4·¼·r4 - ⅕·r5] | 2·cos θ | ·dθ |
| 0 | 0 |
| Iz = | 2·M V | ∫ | π/2 | [(2·cos θ)4 - ⅕·(2·cos θ)5]·dθ |
| 0 |
| Iz = | 2·M V | ∫ | π/2 | (16·cos4 θ - ⅕·32·cos5 θ)·dθ |
| 0 |
| Iz = | 32·M V | ∫ | π/2 | (cos4 θ - ⅖·cos5 θ)·dθ |
| 0 |
| Iz = | 32·M V | ∫ | π/2 | [(1 - sen² θ)·cos² θ - ⅖·cos θ·(1 - sen² θ)²]·dθ |
| 0 |
| Iz = | 32·M V | ∫ | π/2 | [cos² θ - sen² θ·cos² θ - ⅖·cos θ·(1 - 2·sen² θ + sen4 θ)]·dθ |
| 0 |
| Iz = | 32·M V | ∫ | π/2 | [cos² θ - (2·½·sen θ·cos θ)² - ⅖·cos θ·(1 - 2·sen² θ + sen4 θ)]·dθ |
| 0 |
| Iz = | 32·M V | ∫ | π/2 | [cos² θ - 4·sen² 2·θ - ⅖·cos θ·(1 - 2·sen² θ + sen4 θ)]·dθ |
| 0 |
| Iz = | 32·M V | ∫ | π/2 | (cos² θ - 4·sen² 2·θ)·dθ - | 64·M 5·V | ∫ | π/2 | (1 - 2·sen² θ + sen4 θ)·d(sen θ) |
| 0 | 0 |
| Iz = | 32·M V | ·[(½·θ + ½·sen θ·cos θ) - 4·(2·½·θ - ½·sen 2·θ·cos 2·θ)] | π/2 | - | 64·M 5·V | ·[sen θ - 2·⅓·sen³ θ + ⅕·sen5 θ] | π/2 |
| 0 | 0 |
| Iz = | 32·M V | ·{[½·(π/2 + sen π/2·cos π/2) - 4·(π/2 - ½·sen 2·π/2·cos 2·π/2)] - [½·(0 + sen 0·cos 0) - 4·(0 - ½·sen 2·0·cos 2·0)]} - |
| - | 64·M 5·V | ·[(sen π/2 - ⅔·sen³ π/2 + ⅕·sen5 π/2) - (sen 0 - ⅔·sen³ 0 + ⅕·sen5 0)] |
| Iz = | 32·M V | ·(½·π/2 - 4·π/2) - | 64·M 5·V | ·(1 - ⅔ + ⅕) |
| Iz = | 32·M V | ·(¼·π - 2·π) - | 64·M 5·V | ·( | 15 - 10 + 3 15 | ) |
| Iz = | 32·M V | · | -7·π 4 | - | 64·M 5·V | · | 8 15 |
| Iz = (-56·π - | 512 75 | )· | M V |
Resultado, el momento de inercia del sólido es:
| Iz = 8·(-7·π - | 64 | )· | M |
| 75 | 4·(π - 16/9) |
| Iz = | 525·π + 64 | · | 2·M |
| 75 | (-9·π - 16)/9 |
| Iz = | 525·π + 64 | · | 6·M |
| 25 | -9·π - 16 |
| Iz = | 6·M | · | 525·π + 64 |
| 25 | -9·π - 16 |
- ‹ Anterior
- |
- Regresar a la guía TP08
- |
- Siguiente ›
Autor: Ricardo Santiago Netto (Administrador de Fisicanet)
San Martín. Buenos Aires. Argentina.
Ver condiciones para uso de los contenidos de fisicanet.com.ar