Problema nº 3 de teorema de Stokes en una superficie - TP10
Enunciado del ejercicio nº 3
Verificar el teorema de Stokes si F = (x, y, z) y S es la superficie x² + y² = 1, z ≥ 0.
Desarrollo
Fórmulas:
∫∂S F·dC = ∬S rot F·dS
dC = C'(t)·dt
dS = (Xᵤ ∧ Xᵥ)·du·dv
| rot F = | E₁ | -E₂ | E₃ |
| ∂/∂x | ∂/∂y | ∂/∂z | |
| f₁ | f₂ | f₃ |
Solución
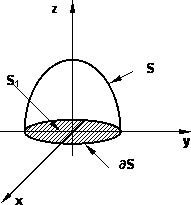
Gráfico del dominio para el cálculo de la superficie
Parametrizamos la superficie S:
X(u, v) = (u, v, 0), u² + v² ≤ 1
Calculamos n:
Xᵤ = (1, 0, 0)
Xᵥ = (0, 1, 0)
| n = Xᵤ ∧ Xᵥ = | E₁ | -E₂ | E₃ |
| 1 | 0 | 0 | |
| 0 | 1 | 0 |
n apunta hacia z > 0.
Hallamos el rot F:
| rot F = | E₁ | -E₂ | E₃ |
| ∂/∂x | ∂/∂y | ∂/∂z | |
| x | y | z |
| rot F = | ∂y | - | ∂x | , - | ∂y | + | ∂z | , | ∂x | + | ∂z |
| ∂y | ∂z | ∂x | ∂z | ∂x | ∂y |
rot F = (1 - 0, -0 + 1, 1 - 0)
rot F = (1, 1, 1)
Planteamos la integral del segundo miembro:
∬SC rot F·dS = ∬S1 rot F·dS
∬SC rot F·dS = ∬D (1, 1, 1)·(0, 0, 1)·du·dv
∬SC rot F·dS = ∬D du·dv
Pasando a sistema de coordenadas polares:
| u = r·cos θ v = r·sen θ | ⟶ |J| = r ⟶ | 0 ≤ r ≤ 1 0 ≤ θ ≤ 2·π |
| = ∫ | 2·π | dθ∫ | 1 | r·dr = |
| 0 | 0 |
| = 2·π·(½·r²) | 1 | = |
| 0 |
= 2·π·(½·1² - ½·0²) =
= 2·π·½ = π
Para el primer miembro parametrizamos la frontera de S, es decir ∂S:
C = (cos t, sen t, 0), 0 ≤ t ≤ 2·π
Preparamos las partes de la integral:
C' = (-sen t, cos t, 0)
F(C(t)) = (0, cos t, sen t)
Planteamos la integral del primer miembro:
| ∫∂S F·dC = ∫ | a | F(C(t))·C'(t)·dt = |
| b |
| = ∫ | 2·π | (0, cos t, sen t)·(-sen t, cos t, 0)·dt = |
| 0 |
| = ∫ | 2·π | cos² t·dt = |
| 0 |
| = ½·t + ½·sen t·cos t | 2·π | = ½·2·π |
| 0 |
∫∂S F·dC = π
Verificado
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP10
- | Siguiente ›
Ejemplo, cómo verificar el teorema de Stokes en una superficie