Ejercicio resuelto de integrales superficiales
Resolver los siguientes ejercicios
Fórmulas aplicables:
∬S f(X)·dσ = ∬D f(X(u, v))·||Xᵤ ∧ Xᵥ||·du·dv
| XG = | ∬S x·dσ |
| ∬S dσ |
| YG = | ∬S y·dσ |
| ∬S dσ |
| ZG = | ∬S z·dσ |
| ∬S dσ |
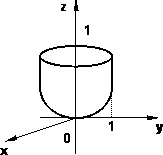
Gráfico de la superficie para calcular el baricentro
Ejercicio: Calcular las coordenadas del baricentro de la superficie:
z = x² + y²
Para:
z ≤ 1
Solución
Como la superficie presenta simetría del dominio con respecto a los planos y = 0 y x = 0, y la integranda presenta antisimetría con respecto a los mismos planos, resulta:
XG = YG = 0
Luego:
| ZG = | ∬S z·dσ | = | I |
| ∬S dσ | AD |
Primero parametrizamos la superficie:
x = u
y = v
z = u² + v²
X(u, v) = (u, v, u² + v²)
Luego hallamos el vector normal a la superficie:
Xᵤ = (1, 0, 2·u)
Xᵥ = (0, 1, 2·v)
| Xᵤ ∧ Xᵥ = (1, 0, 2·u) ∧ (0, 1, 2·v) = | E₁ | E₂ | E₃ | = (-2·u, -2·v, 1) |
| 1 | 0 | 2·u | ||
| 0 | 1 | 2·v |
Xᵤ ∧ Xᵥ = (-2·u, -2·v, 1)
Preparamos las partes para armar la integral:
||Xᵤ ∧ Xᵥ|| = √(-2·u)² + (-2·v)² + 1²
||Xᵤ ∧ Xᵥ|| = √4·u² + 4·v² + 1
||Xᵤ ∧ Xᵥ|| = √4·(u² + v²) + 1
f(X(u, v)) = u² + v²
Armamos la integral:
I = ∬S z·dσ
I = ∬D f(X(u, v))·||Xᵤ ∧ Xᵥ||·du·dv
I = ∬D (u² + v²)·√4·(u² + v²) + 1·du·dv
Como el dominio es una circunferencia de radio = 1 cambiamos a sistema de coordenadas polares:
| u = r·cos θ v = r·sen θ | ⟶ |J| = r ⟶ | 0 ≤ r ≤ 1 0 ≤ θ ≤ 2·π |
I = ∬D (u² + v²)·√4·(u² + v²) + 1·du·dv
I = ∬D' [(r·cos θ)² + (r·sen θ)²]·√4·[(r·cos θ)² + (r·sen θ)²] + 1·r·dr·dθ
Resolvemos:
I = ∬D' (r²·cos² θ + r²·sen² θ)·√4·(r²·cos² θ + r²·sen² θ) + 1·r·dr·dθ
I = ∬D' r²·(cos² θ + sen² θ)·√4·r²·(cos² θ + sen² θ) + 1·r·dr·dθ
I = ∬D' r³·√4·r² + 1·dr·dθ
| I = ∫ | 2·π | dθ∫ | 1 | r³·√4·r² + 1·dr |
| 0 | 0 |
Aplicando un cambio de variable:
w² = 4·r² + 1
r² = ¼·(w² - 1)
w = √4·r² + 1
2·w·dw = 8·r·dr ⇒ ¼·w·dw = r·dr
| I = 2·π·∫ | 1 | r²·√4·r² + 1·r·dr |
| 0 |
| I = 2·π·∫ | w² - 1 4 | ·√w²·¼·w·dw |
I = ⅛·π·∫(w² - 1)·w·w·dw
I = ⅛·π·∫(w² - 1)·w²·dw
I = ⅛·π·∫(w⁴ - w²)·dw
I = ⅛·π·(⅕·w⁵ - ⅓·w³)
| I = ⅛·π·[ | 3·(√4·r² + 1)⁵ - 5·(√4·r² + 1)³ 15 | ] | 1 |
| 0 |
| I = ⅛·π·[ | 3·√(4·r² + 1)⁵ - 5·√(4·r² + 1)³ 15 | ] | 1 |
| 0 |
| I = ⅛·π· | 3·√5⁵ - 3·√1 - (5·√5³ - 5·√1) 15 |
| I = ⅛·π· | 3·5²·√5 - 3 - (5·5·√5 - 5) 15 |
| I = ⅛·π· | 75·√5 - 3 - 25·√5 + 5 15 |
| I = ⅛·π· | 50·√5 + 2 15 |
| I = ⅛·π·2· | 25·√5 + 1 15 |
| I = ¼·π· | 25·√5 + 1 15 |
Para el denominador:
AD = ∬S dσ = ∬D ||Xᵤ ∧ Xᵥ||·du·dv
AD = ∬D √4·(u² + v²) + 1·du·dv
Como el dominio es una circunferencia de radio = 1 cambiamos a sistema de coordenadas polares:
| u = r·cos θ v = r·sen θ | ⟶ |J| = r ⟶ | 0 ≤ r ≤ 1 0 ≤ θ ≤ 2·π |
AD = ∬D √4·(u² + v²) + 1·du·dv
AD = ∬D' √4·[(r·cos θ)² + (r·sen θ)²] + 1·r·dr·dθ
Resolvemos:
AD = ∬D' √4·(r²·cos² θ + r²·sen² θ) + 1·r·dr·dθ
AD = ∬D' √4·r²·(cos² θ + sen² θ) + 1·r·dr·dθ
AD = ∬D' r·√4·r² + 1·dr·dθ
| AD = ∫ | 2·π | dθ∫ | 1 | r·√4·r² + 1·dr |
| 0 | 0 |
| AD = 2·π·∫ | 1 | r·√4·r² + 1·dr |
| 0 |
Mediante un cambio de variable:
w = 4·r² + 1
dw = 8·r·dr
⅛·dw = r·dr
| AD = 2·π·∫ | 1 | r·√4·r² + 1·dr |
| 0 |
AD = 2·π·∫ ⅛·√w·dw
AD = 2·π·⅛·∫ w½·dw
AD = ¼·π·∫ w½·dw
| AD = ¼·π· | w½ + 1 | = ¼·π· | w3/2 |
| ½ + 1 | 3/2 |
AD = ¼·π·2·⅓·√w³ = ⅙·π·√w³
| AD = ⅙·π·√(4·r² + 1)³ | 1 |
| 0 |
AD = ⅙·π·(√(4·1² + 1)³ - √(4·0² + 1)³)
AD = ⅙·π·(√(4 + 1)³ - √(1)³)
AD = ⅙·π·(√5³ - √1)
AD = ⅙·π·(√5³ - 1)
AD = ⅙·π·(5·√5 - 1)
La coordenada es:
| ZG = | I |
| AD |
| π | · | 25·√5 + 1 | |
| ZG = | |||
| 4 | 15 | ||
| π | · | 5·√5 - 1 | |
| 6 |
| ZG = | π | · | 25·√5 + 1 | · | 6 | · | 1 |
| 4 | 15 | π | 5·√5 - 1 |
| ZG = | 3 | · | 25·√5 + 1 | · | 1 |
| 2 | 15 | 5·√5 - 1 |
| ZG = | 25·√5 + 1 | · | 1 |
| 10 | 5·√5 - 1 |
| ZG = | 25·√5 + 1 |
| 10·(5·√5 - 1) |
El baricentro es:
| G = [0, 0, | 25·√5 + 1 | ] |
| 10·(5·√5 - 1) |
• Fuente:
"Lecciones de análisis II" del Dr. Alfredo F. Novelli para Análisis Matemático II de UNLu.
Autor: Ricardo Santiago Netto. Argentina