Guía n° 12 de ejercicios de integrales dobles (cuarta parte)
Resolver los siguientes ejercicios
� Ver resolución de los ejercicios al pie de la página
Calcular las coordenadas del baricentro de los siguientes dominios planos:
Problema n° 13
Calcular el baricentro del dominio plano limitado por las curvas:
√x + √y = √a (a > 0)
x = 0
y = 0
Problema n° 14
Calcular el baricentro del dominio plano D representado en la figura siguiente, donde la curva representa la circunferencia de centro en (1,1) y radio 1:
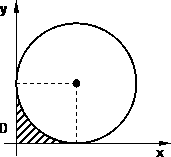
Gráfico del dominio para el cálculo de baricentro
Problema n° 15
Calcular el baricentro del dominio plano encerrado por la cardioide r = 1 - cos θ.
Problema n° 16
r ≤ 1 - sen θ, 0 ≤ θ ≤ 2·π
Problema n° 17
r ≤ 2·(1 - cos θ), 0 ≤ θ ≤ 2·π
Problema n° 18
r ≤ 2·θ, 0 ≤ θ ≤ π
Problema n° 19
2·cos θ ≤ r ≤ 1 + cos θ, 0 ≤ θ ≤ π
Problema n° 20
r ≤ 1 + cos θ, r ≤ 3·cos θ
• Fuente:
"Lecciones de análisis II" del Dr. Alfredo F. Novelli para Análisis Matemático II de UNLu.
Autor: Ricardo Santiago Netto. Argentina