Sucesiones y series de números reales

Teorema de amplitud de ℜ

Toda sucesión de Cauchy en ℜ es convergente (el espacio métrico ℜ d(x, y) = |x - y| es completo).

• Demostración:

Sea (x_n) de Cauchy. Entonces es acotada y, por tanto, tiene algún valor de adherencia. Con lo que acabamos de ver, bastará probar que ese valor de adherencia es único.

Supongamos que a y b fueran valores de adherencia distintos de (x_n). Sea ε = |a - b|/3

En ]a - ε, a + ε[ y en ]b - ε, b + ε[ hay infinitos términos de la sucesión.

Por tanto, existen infinitos p, q ∈ N tales que: |x_p-x_q| > ε y x_n no sería de Cauchy.

Definición:

Se dice (x_n) es monótona creciente (decreciente) cuando, ∀ n ∈ N, x_n ≤ x_{n + 1} (respectivamente x_n ≥ x_{n + 1}), la monotonía se dice que es estricta cuando el signo es < (respectivamente >)

• Proposición:

Toda sucesión monótona y acotada es convergente. Además, si es creciente lim (x_n) = sup {x_n/n ∈ N}, si es decreciente lim (x_n) = inf. {x_n /n ∈ N}

• Demostración:

Supongamos que (x_n) es creciente y acotada. Sea a el sup {x_n /n ∈ N}

De la definición de sup. se sigue que:

• La derecha de a no hay ningún x_n
• ∀ ε > 0, a la derecha de a - ε hay algún x_n. Sea este el x_υ. Entonces por ser (x_n) creciente,

n > υ ⇒ a - ε < x_n ≤ a

|x_n - a| < ε (c.q.d.)

Notación:

lim (x_n) = a ⇔ (x_n) → a

Para indicar que (x_n) es creciente y que a es su límite se puede escribir: (x_n) ↗ a.

Para indicar que es decreciente y que a es su límite: (x_n) ↘ a.

Supongamos que (x_n) es acotada, además tiene algún punto de adherencia.

El conjunto de los valores de adherencia es por tanto acotado. Además el conjunto de los valores de adherencia de cualquier sucesión es un conjunto acotado (podría ser Ø).

Por tanto, el conjunto de los valores de adherencia de una sucesión acotada es un conjunto no vacío, cerrado y acotado (compacto).

Por ser ese conjunto compacto y no vacío existen el mínimo y el máximo de sus adherentes. Por definición, este mínimo y máximo son el límite inferior y el límite superior de (x_n).

Ejemplo n° 1

Supongamos que (x_n) es una sucesión acotada.

Demostrar que límite inferior (x_n) = sup {inf{x₀, x₁, x₂, ……}, inf{x₁, x₂, ………}, inf{x₂, …} …}

lim sup (x_n) = inf {sup {x₀, x₁, …}, sup {x₁, x₂, …}, sup {x₂, x₃, ………} …}

Indicación:

Por ser x_n acotada existen esos inf's y sup's la sucesión (inf{x₀, x₁, …}, inf{x₁, x₂, …} …) es monótona creciente.

Suponemos: lim inf (x_n) = sup [inf {x₀, x₁, x₂, …}, inf {x₁, x₂, …} …] = α

Todos los inf's están en (-4, α) y en (α + ε, α) hay algún inf pues sino, α no sería el límite, pero al ser la sucesión de inf's es creciente, en este último intervalo están todos los inf's salvo finitos. Falta Acabarlo.

Algunos ejemplos interesantes de límites:

∀ a > 0, lim ⁿ√a = 1

Si a = 1 evidente.

Si a > 1 escribimos x_n = ⁿ√a - 1

Se trata de probar que (x_n) → 0

(x_n + 1)ⁿ = 1 + (ⁿ₁) x_n + (ⁿ₂) x_n² + ……… > 1 + n·x_n ⇒ x_n < (a - 1)/n → 0

Ejemplo n° 2

Verlo para a < 1 (Indicación: tomar 1/a)

lim ⁿ√n = 1

n = (ⁿ√n - 1 + 1)ⁿ = 1 + (ⁿ₁)·(ⁿ√n - 1) + (ⁿ₂)·(ⁿ√n - 1)² + …… > 1 + [n·(n - 1)/2]·(ⁿ√n - 1)² ⇒ 0 ≤ (ⁿ√n - 1)² ≤ 2/(n + 1) → 0

Ejemplo n° 3

Ver que (ⁿ√n - 1)² → 0 ⇒ (ⁿ√n - 1) → 0

• limⁿ√n^p = 1
• ∀ a > 1, ∀ p, lim n^p/aⁿ = 0

Dice que la "exponencial" puede con la "potencial": el producto de ambas va a donde manda la exponencial. Si p < 0 evidente. Si p > 0 el numerador va a +4 y el denominador también.

n^p (1/aⁿ) → 0

b, p > 0, n^p/(1 + b)ⁿ → 0

Falta acabarlo.

Límites infinitos:

Aunque cuando hablamos de la convergencia, o del límite, de una sucesión, dicha convergencia o dicho límite, es a (un) n° real, a veces también se habla de convergencia a +4 ó -4 (de límites infinitos) El contexto suele dejar claro si se están admitiendo "límites infinitos".

Definición:

(x_n) converge a +4 (-4) cuando,

∀ ρ ∈ ℜ, ∑ υ ∃ N /n > υ ⇒ x_n > ρ (respectivamente x_n < ρ)

Ejemplos:

(1, 2, 3, ……) → +4

(1, 3, 2, 4, 3, 5, 4, 6, 5, 7, 6, 8, ………) → +4

La primera de esas sucesiones es monótona creciente y no acotada, es evidente que cualquier sucesión de este tipo "converge" a +4.

La segunda no es monótona.

(1, 2, 1, 3, 1, 4, ……) no converge a nada, ni a un número, ni a +4 ni a - 4.

Por lo mismo, a veces se admiten como valores de adherencia (en particular, como "límite inf" ó "límite sup") a +4 y -4.

Definición:

+4 (-4) es valor de adherencia de (x_n) cuando, ∀ ρ ∈ ℜ, ∀ υ ∈ N, ∃ n > υ / x_n > ρ (respectivamente x_n < ρ)

Si un sucesión es no acotada superiormente (inferiormente) su límite superior (inferior) es +4 (-4).

lim sup (1, 2, 1, 3, 1, 4, ……) = +4

lim inf (1, 2, 1, 3, 1, 4, ……) = 1

lim inf (1, 2, 3, ………) = +4 porque sólo tiene como valor de adherencia +4 = lim sup. (1, 2, 3, …)

Con este acuerdo (admitir +4 y -4 como posibles valores de adherencia), se verifica:

• Toda sucesión (acotada o no) tiene algún valor de adherencia
• Toda sucesión (acotada o no) tiene lim inf y sup

R¯ = ℜ ∪ {-4, +4}

Es muy fácil ver que:

(x_n) → +4, (y_n) → a (-4 < a ≤ +4) ⇒ (x_n + y_n) → +4

(x_n) → +4, (y_n) es acotada inferiormente ⇒ (x_n + y_n) → +4

(x_n) → +4, (y_n) → a (a ≠ 0) ⇒ (x_n·y_n) → +4 si 0 < a ≤ +4

-4 si -4 ≤ a < 0

(x_n) → +4, (y_n) está acotada inferiormente por a > 0 (superiormente por a < 0) ⇒ (x_n·y_n) → +4 (respectivamente -4)

Sin embargo,

Si (x_n) → +4 e (y_n) → -4, entonces a (x_n + y_n) le puede pasar cualquier cosa.

Ejemplos:

(x_n) = (1, 2, 3, ……), (y_n) = (-1, -2, -3, …), (x_n + y_n) = (0, 0, 0, ……) → 0

(x_n) = (1, 2, 3, ……), (y_n) = (-2, -4, -6, …), (x_n + y_n) = (-1, -2, -3, ……) → -4

(x_n) = (1, 2, 3, …), (y_n) = (-2, -1, -5, -2, -8, -3, ……), (x_n + y_n) = (-1, 1, -2, 2, -3, 3, …) no converge a nada.

Si (x_n) → +4 (-4) e (y_n) → 0 entonces (x_n + y_n) cualquier cosa:

(1,2, 3, ……) (1, ½, ⅓, ……) = (1, 1, 1, ……) → 1

(1,2, 3, ……) (1, ½², ⅓², ……) = (1, ½, ⅓, ……) → 0

(1,2, 3, ……) (1, 1/√2, 1/√3, …) = (1, √2, √3, ……) → +4

(1, 2, 3, …) (1, ½², 1/√3,¼², 1/√5,1/6², 1/√7, ……) = (1, ½, √3,¼, √5, ……)

Series numéricas:

Vamos a tratar de dar sentido a las sumas infinitas (infinitos numerables sumandos).

x₁ + x₂ + ………… + x_n + …… donde los x_k son números reales.

Para ello sea (x_n) una sucesión de números reales a partir de ella construimos la sucesión de sumas parciales de aquella:

(x₁, x₁ + x₂, x₁ + x₂ + x₃, ……), la cual se suele llamar serie de términos (x₁, x₂, x₃, …) y denotar: ⁴∑_{n = 1}x_n.

Definición:

La serie ⁴∑_{n = 1}x_n se dice sumable, o convergente, a a ∈ ℜ cuando la sucesión de sumas parciales (x₁, x₁ + x₂, x₁ + x₂ + x₃ …) es convergente a a.

Es decir, cuando, ∀ ε > 0, ∑ υ ∃ N /n > υ ⇒ |ⁿ ∑_{k = 1} x_k - a| < ε

• Proposición:

⁴∑_{n = 1} es sumable si sólo si es de Cauchy, es decir, tal que,

∀ ε > 0, ∑ υ ∃ N / υ < p < q ⇒ |^q ∑_{k = p} x_k| < ε

• Demostración:

Si ⁴∑_{n = 1}x_n es sumable entonces:

∀ ε > 0, ∑ υ ∃ N /n > υ ⇒ |ⁿ ∑_{k = 1} x_k - a| < ε,

Es decir, es convergente a a, por consiguiente es de Cauchy, así pues:

∀ ε > 0, ∑ υ ∃ N / p, q > υ ⇒ |^q ∑_{k = p} x_k| < ε

Corolario:

Condición necesaria para que la serie ⁴∑_{n = 1}x_n sea sumable es que la sucesión de sus términos converja a cero, lim (x_n) = 0.

• Demostración:

Tómese q = p es la proposición anterior (Verlo)

⁴∑_{n = 1}x_n es sumable ⇒ (x_n) → 0

Veamos que el recíproco no se da en alguno de los ejemplos que siguen:

Ejemplos:

1) (x_n) = (1, 1, 1, ……) la sucesión de sumas parciales es (1, 2, 3, ……)

2) (x_n) = (1, -1, 1, -1, …) la sucesión de sumas parciales es (1, 0, 1, 0, 1, 0, ……) no convergente. En otras palabras, la serie ⁴∑_{n = 1}(-1)^{n + 1} no es sumable.
En ambos casos (x_n) no converge a 0, en el 1° converge a 1 y en el segundo no converge a nada, pues lim inf ≠ lim sup

3) ⁴∑_{n = 1}½ⁿ Como hemos dicho, será sumable si la sucesión de sumas parciales (ⁿ ∑_{k = 1}½^k) es convergente (2, ½ + ¼, ½ + ¼ + ⅛, …). El término n-ésimo de estas sumas parciales es la suma de una progresión geométrica de primer término ½ y razón ½

ⁿ ∑_{k = 1} ½^k = ½ + ½² + ½³ + …… + ½ⁿ = (1^er término - siguiente al último)/(1-razón) = (½ - ½^{n + 1})/ ½ = 1 - ½ⁿ → 1

La serie ⁴∑_{n = 1}½ⁿ es sumable y su suma es 1.

Naturalmente (½ⁿ) → 0

Ejemplo n° 4

Estudiar la sumabilidad de las series geométricas ⁴∑_{n = 0} a·rⁿ, donde a, r ∈ ℜ. Si a = 0 evidente.

Si a ≠ 0 ver que la serie es sumable si sólo si |r| < 1. Ver que, en dicho caso, la suma es a/(1 - r).

(a·r, a·r + a·r², a·r + a·r² + a·r³, ……) El término n-ésimo de estas sumas parciales es la suma de una progresión geométrica:

ⁿ ∑_{k = 1} a·r^k = a·r + a·r² + ……… + a·rⁿ = (a·r - a·r^{n + 1})/(1 - r) = (a/(1 - r)) (r - r^{n + 1}) se utiliza |r| < 1 → a/(1 - r)

4) la serie armónica:

⁴∑_{n = 1}1/n se verifica que 1/n → 0, luego puede ser sumable.

A diferencia del caso anterior, no conocemos una fórmula que nos diga cuanto vale.

1 + ½ + ……… + 1/n = ⁿ ∑_{k = 1} 1/k

1 + ½ + ⅓ + ¼ + ⅕ + ⅙ + ⅐ + ⅛ + ⅑ + …… + 1/15 + 1/16 + 1/17

S₁ = 1 > ½

S₂ = 1 + ½ > 2/2

S₄ > 3/2

S₈ > 4/2

S₁₆ > 5/2

S_n > (n + 1)/2

Por otra parte como los términos de esta serie son positivo, la sucesión de sumas parciales es monótona creciente: S₁ < S₂ < S₃ < … y ocurre que sustracción S₁ < S₂ < S₄ < S₈ < … va a +4 Luego (S_n) va a +4 ⇒ la serie no es sumable.

Este ejemplo de serie armónica nos falla para poder afirmar que (x_n) → 0 no implica ⁴∑_{n = 1}x_n sumable

La serie ⁴∑_{n = 1}x_n es sumable o convergente, cuando su sucesión de sumas parciales: (s₁, s₂, s₃, ……) = (x₁, x₁ + x₂, x₁ + x₂ + x₃, ………) es convergente. En dicho caso, al límite de esta sucesión se llama suma de serie y se suele representar de la misma forma que la serie ⁴∑_{n = 1}x_n

Ya el contexto dice de lo que hablamos es la serie, o caso de ser sumable de su suma.

Vimos que: ⁴∑_{n = 1}x_n es sumable ⇔ (x_n) → 0 y que el recíproco es falso.

Ejemplo n° 5

La serie armónica ⁴∑_{n = 1}1/n no es sumable, aunque (1/n) → 0

Un ejemplo sorprendente: La serie ⁴∑_{n = 1}1/n "n sin ceros" la expresión decimal de n no tiene ningún cero: 1 + ½ + …… + ⅑ + 1/11 + …… + 1/99 + 1/111 + 1/112 + ………

Pues bien ocurre que la serie armónica "suma" +4 (no es sumable) mientras que esta sí lo es y su suma es menor que 90.

Veámoslo:

Términos 1/n con n de una cifra hay 9, todos ≤ 1

Términos 1/n con n de dos cifras hay 9², todos < ⅒

Términos 1/n con n de tres cifras hay 9³, todos < 1/100

……………………………………………………………………………

Sea (s₁, s₂, ……) la sucesión de sumas parciales de la serie. Como los términos son positivos, la sucesión es creciente s₁ < s₂ < s₃ < … Por tanto, es sumable si sólo si es acotada. Es acotada si sólo si lo es alguna de la sucesión:

S₉ < 9, s_{9 + 9}² < 9 + 9²/10, s_{9 + 9}²₊₉³ < 9 + 9²/10 + 9³/100, s_n < 9 + 9²/10 + … + 9ⁿ/10^{n - 1}, esto es una progresión geométrica de primer término 9 y de razón 9/10.

(9-9^{n + 1}/10ⁿ)/(1 - 9/10) → n → 4 9/(1-9/10) ⇒ lim (S_{9+ …… +9}ⁿ) = sup {s_{9+ …… + 9}ⁿ /n ∈ N} < 90

lim S_n ⇒ sup {s_n /n ∈ N} < 90

Es desconcertante porque parece que quitamos pocos términos, de los 9 primeros no quitamos ninguno, de los 90 siguientes 9, de los 900 siguientes 171, …………

Ejemplo n° 6

Sabiendo que ⁴∑_{n = 1}1/n no es sumable ("suma" +4) ver que tampoco es ⁴∑_{n = 1}1/(an + b), donde a, b > 0

Indicación, la sucesión de sumas parciales de esto es creciente como la de la anterior. En las sucesiones convergentes es lo mismo que ser acotada.

¿Qué ocurre en la sucesión armónica generalizada ⁴∑_{n = 1}1/n^p?

Si p < 1 1/n < 1/n^p luego 1 + ½ + …… + 1/n < 1 + ½^p + …… + 1/n^p

Si p ≤ 1 la serie no es sumable ("suma" +4)

Si p > 1 tenemos 1/n^p < 1/n aquel argumento no vale (el que la grande vaya a +4 no implica nada). Vamos a ver que cuando p > 1 ⁴∑_{n = 1}1/n^p es sumable.

1 + ½^p + ⅓^p + ¼^p + 1/5^p + ⅙^p + ⅐^p + ⅛^p + …… + 1/15^p + 1/16^p + …… + 1/31^p + …

S₁ = 1

S_{1 + 2} < 1 + 2/2^p

S_{1 + 2 + 2}² < 1 + 2/2^p + 4/4^p

…………………………………

S_{1 + 2 + …… + 2}ⁿ < 1 + ½^{p - 1} + ¼^{p - 1} + ⅛^{p - 1} + … + 1/(2^{p - 1})ⁿ = 1 + 1/(2^{p - 1}) + 1/(2^{p - 1})² + … + 1/(2^{p - 1})ⁿ = [1 - 1/(2^{p - 1})^{n + 1}]/(1 - 2^{p - 1}) → n → 4 1/(1 - 2^{p - 1})

Progresión geométrica de primer término 1 y de razón ½^{p - 1} < 1, luego la sucesión (s_{1 + 2 + … + 2}ⁿ) es acotada ⇒ (s_n) es creciente y acotada ⇒ es convergente.

Una cosa que nos olvidamos ver en el capítulos de sucesiones:

• Ver que a ∈ A¯ si sólo si a es límite de alguna sucesión cuyos términos son de A (Indicación: trivialmente, si a ∈ A, entonces a es límite de (a, a, a, …), en otro caso, es decir, cuando a ∈ A¯ / A, resulta que a ∉ A y estamos en el caso siguiente)
• Ver que a ∈ A' si solo si a es límite de una sucesión cuyos términos son de A y todos distintos, (equivalentemente, todos distintos de a)

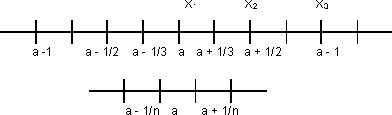
x_n ∈ ]a - 1/n, a + 1/n[, x_n ≠ x₁, x₂, x₃, ……, x_n-1

• ‹ Anterior
• |
• Siguiente ›

Autor: Daniel Fernández

España.

Editor: Ricardo Santiago Netto (Administrador de Fisicanet)

Ver condiciones para uso de los contenidos de fisicanet.com.ar

• 🔍
• ✉ f t