La demostración que no cupo en el márgen de la aritmética de Diofanto
El conocimiento del teorema de Pitágoras es milenario y no obstante que ha sido demostrado en muchas formas diferentes y de que aparentemente ya se conoce todo al respecto, muchas propiedades sorprendentes de la ecuación Pitagórica han permanecido ocultas.
En este trabajo se definen las relaciones entre los valores de los números base es decir los catetos y la hipotenusa (a, b, c) de los correspondientes triángulos rectángulos y que satisfacen a² + b² = c², c = b + k un método que constituye la solución completa de dicha ecuación.
La nueva solución está basada en el origen numérico de la ecuación y corrige la antigua y simplista clasificación para las llamadas "ternas pitagóricas primitivas", también unifica bajo un criterio generalizado las leyes que rigen sus diferentes parámetros de conformación.
Si (a, b, c) satisfacen a² + b² = c², c = b + k entonces existen infinitas ternas Pitagóricas con diferente configuración, así:
[a, b, (b + 1)], [a, b, (b + 2)], [a, b, (b + 8)], [a, b, (b + k)]
Actualmente, bajo el criterio vigente, para asignar a una terna la categoría de ¡primitiva! Es suficiente que la terna satisfaga las siguientes dos condiciones.
a² + b² = (b + k)²; mcd[a, b, (b + k)] = 1
Enseguida muestro varios conjuntos de terna Pitagóricas con diferentes valores de (c - b).

Continuando de la misma forma podremos apreciar que la secuencia de (c - b) es decir, las diferencias entre las magnitudes correspondientes a la hipotenusa y el cateto mayor es:
1, 2, 8, 18, 25, 32, 49, 50, 72, 81, 98, 121, 126, 158, 194, …,
El patrón general para la conformación de la ecuación
Si (a, b, c) satisfacen a² + b² = c², entonces (c - b) puede ser un entero par o impar, es impar, sí y solo si, es igual a {1, 9, 25, 49, 81, 121, 169, …, es decir, el cuadrado de cualquier número impar.
Es par, sí y solo si, es igual a {2, 8, 18, 32, 50, 72, 98, …,
Para los pares podemos apreciar que cada número se conforma sumándole al número anterior la diferencia entre este mismo número y su precedente más 4 unidades.
Si denominamos m a la diferencia (c - b). Entonces:
m₍ₙ ₊ ₁₎ = mₙ + (mₙ - m₍ₙ ₋ ¹₎ + 4)
La siguiente es una forma sencilla que encontré para hallar tales números:
| 2 | 6 | 10 | 14 | 18 | 22 | 26 | 28 | 32 | 36 | |||||||||
| 2 | 8 | 18 | 32 | 50 | 72 | 98 | 126 | 158 |
La fila superior es una sucesión con incremento de 4. En la fila inferior, partiendo de 2 aparecen los números buscados, para obtener el número siguiente basta sumar al precedente el número inmediato a su derecha en la fila superior.
La solución ancestral para la ecuación a² + b² = c²
Sí (a, b, c) son enteros diferentes de cero, que satisfacen:
a² + b² = c² (1.1)
Considerando los valores absolutos |a|, |b|, |c|, estos números son las longitudes de los lados de un triángulo rectángulo.
Para determinar todas las soluciones enteras no triviales de (1.1), basta determinar las llamadas ternas pitagóricas primitivas (a, b, c):
(a, b, c) > 0, mcd(a, b, c) = 1, a par
El siguiente teorema da una descripción completa de las denominadas ternas primitivas:
Teorema (1-A):
Si (u, v), son enteros diferentes de cero y de paridad diferente y si:
(a = 2·u·v), (b = u² - v²), (c = u² + v²)
Entonces la terna (a, b, c) es denominada Pitagórica primitiva.
La verdadera y completa solución
Demostraremos que una terna Pitagórica es "original" sí y solo si satisface los parámetros que posteriormente serán definidos.
Tales parámetros determinan que las ternas originales se configuran exclusivamente en la forma.
(x, y, z) de manera que x² + y² = (y + 1)²
Bajo el criterio actualmente vigente (a < b) es par y b es impar mientras que en el nuevo x puede ser menor o mayor que y, lo mismo que par o impar.
Cuando n es una fracción la llamo fracción generatriz y la represento como p/q.
Teorema (1):
Para cada n = [1, 2, 3, 4, 5, …, ∞] existen tres números enteros (x, y, z) que satisfacen las siguientes condiciones: x² + y² = z²
Donde (X = 2·n + 1), [Y = 2·n·(n + 1)], [Z = 2·n·(n + 1) + 1]
Las siguientes ternas, x, y, z, en las cuales z = (y + 1), satisfacen: x² + y² = z²
{(3, 4, 5), (5, 12, 13), (7, 24, 25), (9, 40, 41), (11, 60, 61), (13, 84, 85), …, losnúmeros subrayados {4, 12, 24, 40, 60, 84, 112, …, son las magnitudes correspondientes al lado y para todo triángulo cuyos lados [x, y, (y + 1)] satisfacen x² + y² = (y + 1)²
En la siguiente tabla se muestra que tales magnitudes son iguales a 4 multiplicado por la suma de enteros consecutivos entre 1 y n.
| 4 = 4·(0 + 1) …………… 12 = 4·(1 + 2) …………… 24 = 4·(1 + 2 + 3) ……… 40 = 4·(1 + 2 + 3 + 4) … | n = 1 ⟶ y = 2·n·(n + 1) = 2·1·(1 + 1) n = 2 ⟶ y = 2·n·(n + 1) = 2·2·(2 + 1) n = 3 ⟶ y = 2·n·(n + 1) = 2·3·(3 + 1) n = 4 ⟶ y = 2·n·(n + 1) = 2·4·(4 + 1) |
Por lo tanto para cada n = {1, 2, 3, 4, 5,…, existe una terna [x, y, (y + 1)] que satisface x² + y² = (y + 1)², en la cual y es igual a 4 multiplicado por la suma de todos los enteros consecutivos contenidos entre (1 y n).
Es bien sabido que la suma de una sucesión de enteros positivos entre 1 y n es igual a la mitad del producto de n por su sucesor (n + 1), como se muestra a continuación.
1 + 2 + 3 + 4 + 5 + 6 + 7 … + n = n·(n + 1)/2,
Ejemplo de una sucesión de enteros positivos
Para n = 9:
(1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9) =
| = | n·(n + 1) | = | 9·(9 + 1) | = | 9·10 | = 45 |
| 2 | 2 | 2 |
Por lo tanto y = 4·n·(n + 1)/2 = 2·n·(n + 1), y todo valor de (y = z - 1) en una terna Pitagórica original es igual a 4 multiplicado por un número triangular.
Si y es igual a 2·n·(n + 1), se cumple que:
(X = 2·n + 1), [Y = 2·n·(n + 1)], [Z = 2·n·(n + 1) + 1]
Y la suma de los cuadrados de x e y constituye una identidad con respecto al cuadrado de z.
(X = 2·n + 1)² + [Y = 2·n·(n + 1)]² = [Z = 2·n·(n + 1) + 1]² = 4·n⁴ + 8·n³ + 8·n² + 4·n + 1
Asignándole a n valores entre 1 e infinito, para cada número existen tres valores que corresponden a los tres lados de un triángulo rectángulo.
(m = 2) ⟶ xᵐ + yᵐ = zᵐ = (X = 2·n + 1)² + [Y = 2·n·(n + 1)]² = [Z = 2·n·(n + 1) + 1]² =
= 4·n⁴ + 8·n³ + 8·n² + 4·n + 1
(m ≠ 2) ⟶ = (X = 2·n + 1)ᵐ + [Y = 2·n·(n + 1)]ᵐ ≠ [Z = 2·n·(n + 1) + 1]ᵐ
Como se puede apreciar el teorema de Pitágoras constituye una identidad.
Conformación de las ternas originales fraccionarias
Teorema (2):
Para cada fracción racional p/q, existen tres fracciones racionales (r/q), (b/q²), (c/q²), de tal forma que satisfacen las siguientes ecuaciones:
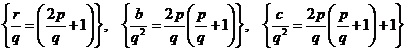
Las ternas (a, b, c) = (45, 28, 53), (55, 48, 73), (95, 68, 193) satisfacen a² + b² = c²
Dividiendo los tres términos de cada una de estas ternas por (c - b) = 25, que es común para las tres, obtenemos respectivamente las siguientes ternas formadas por tres fracciones a las cuales representaremos en forma general como
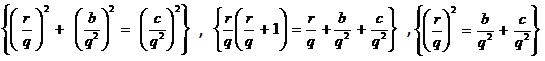
X = (2·n + 1)
X² = (2·n + 1)² = 4·n² + 4·n + 1
Y = 2·n·(n + 1)
Y² = 4·n⁴ + 8·n³ + 4·n²
Z = 2·n·(n + 1) + 1
X² + Y² = 4·n⁴ + 8·n³ + 8·n² + 4·n + 1
4·n⁴ + 8·n³ + 8·n² + 4·n + 1 = 4·n⁴ + 8·n³ + 8·n² + 4·n + 1,
(m = 2) ⟶ xᵐ + yᵐ = zᵐ = (X = 2·n + 1)² + [Y = 2·n·(n + 1)]² = [Z = 2·n·(n + 1) + 1]² =
= 4·n⁴ + 8·n³ + 8·n² + 4·n + 1
Si (m ≠ 2) ⟶ = (X = 2·n + 1)ᵐ + [Y = 2·n·(n + 1)]ᵐ ≠ [Z = 2·n·(n + 1) + 1]ᵐ
Como se puede apreciar el teorema de Pitágoras constituye una identidad.
Y la única posibilidad de que se cumpla es que los términos que representan a los componentes X, Y, Z de la identidad sean cuadráticos.
(m = 2) ⟶ xᵐ + yᵐ = zᵐ = (2·n + 1)² + [2·n·(n + 1)]² = [2·n·(n + 1) + 1]² = 4·n⁴ + 8·n³ + 8·n² + 4·n + 1
(2·n + 1)² + [2·n·(n + 1)]² = [2·n·(n + 1) + 1]²
Para todo número irracional i existe una terna de números irracionales.
X = 2·i + 1, Y = [2·i·(i + 1)], Z = [2·i·(i + 1) + 1], de manera que X² + Y² = Z²
(2·i + 1)² + [2·i·(i + 1)]² = [2·i·(i + 1) + 1]² = 4·n⁴ + 8·n³ + 8·n² + 4·n + 1
X² = (2·Π + 1)², Y² = [2·Π·(Π + 1)]², Z² = [2·Π·(Π + 1) + 1]² ⟶ X² + Y² = Z²
X² = (2·e + 1)², Y² = [2·e·(e + 1)]², Z² = [2·e·(e + 1) + 1]² ⟶ X² + Y² = Z²
X² = (2·φ + 1)², Y² = [2·φ·(φ + 1)]², Z² = [2·φ·(φ + 1) + 1]² ⟶ X² + Y² = Z²
El uso de 7 cifras decimales confiere la suficiente aproximación para todo efecto.
Π = 3,1415926
℮ = 2,7182818
φ = 1,6180339 número Áureo
Email: rubenmore@hotmail.com
Cartagena de Indias. Colombia.
Ingeniero Industrial egresado de la Universidad Tecnológica de Bolivar.
Experto en procesos industriales de polimerización.
Autor: Rubén Moré Argel. Ingeniero Industrial. Colombia.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).