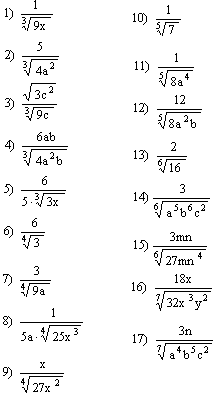Guía nº 14-d de ejercicios de operaciones con números reales

División de radicales

Ejercicios de aplicación

Racionalizar el denominador (1^er Caso) de los siguientes cocientes:

1)	2	=
	√7

2)	1	=
	√3

3)	5	=
	√2

4)	3	=
	√15

5)	12	=
	√6

6)	33	=
	√33

7)	3	=
	4·√5

8)	a	=
	√b

9)	2·a	=
	√2·a·x

10)	5·n²	=
	3·√m·n

11)	2·x·∛4·y	=
	3·y·√2·x

Racionalizar el denominador (2^do Caso) de los siguientes cocientes:

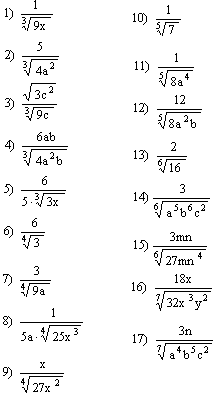
Problemas de potenciación y radicación con números reales

Racionalizar el denominador (3^er Caso) de los siguientes cocientes:

1)	2	=
	√3 - 1

2)	5	=
	4 - √11

3)	2	=
	1 - √7

4)	4	=
	√2 - 1

5)	√2	=
	√2 + 1

6)	2·√3	=
	3 - √5

7)	11	=
	2·√3 - 1

8)	√3 + 1	=
	√3 - 1

9)	5 + √11	=
	5 - √11

10)	3 - √2	=
	1 + √2

11)	5 - √8	=
	√2 - 5

12)	3 + √5	=
	3 - √5

13)	3 + √6	=
	3 - √6

14)	5 + 2·√2	=
	4 - √3

15)	√2 + √3	=
	2 - √3

16)	√5 + √2	=
	2 + √5

17)	3 + 2·√3	=
	3 - 2·√3

18)	4 - √2	=
	2 + 5·√2

19)	√5 + √2	=
	7 + 2·√10

20)	9·√3 - 3·√2	=
	6 - √6

21)	1	=
	√5 + √7

22)	√3	=
	√3 + √5

23)	√7 - √2	=
	√7 + √2

24)	√7 - √5	=
	√5 + √7

25)	√5 + √8	=
	√5 - √8

26)	√2 - √5	=
	√2 + √5

27)	√3 + √2	=
	√3 + √2

28)	√7 + 2·√5	=
	√7 - √5

29)	√2 - 3·√5	=
	2·√2 + √5

30)	2·√5 + √3	=
	2·√5 - √3

31)	√7 - 2·√2	=
	5·√7 - √2

32)	√5 + 3·√2	=
	2·√5 + √2

33)	2·√7 - 3·√5	=
	√7 + 2·√5

34)	19	=
	5·√2 - 4·√3

35)	3·√2	=
	7·√2 - 6·√3

36)	2·√7 + √5	=
	4·√5 - 3·√7

37)	√7 + 3·√11	=
	5·√7 + 4·√11

38)	√5 + 2·√7	=
	4·√5 - 3·√7

39)	5·√2 - 6·√3	=
	4·√2 - 3·√3

40)	2·√3 - 3·√2	=
	2·√3 + 3·√2

41)	4·√3 - 3·√7	=
	2·√3 + 3·√7

42)	5·√2 - 6·√3	=
	4·√2 - 3·√3

Ecuaciones con radicales

Solamente vamos a resolver ecuaciones en las cuales el valor de x se encuentra bajo el signo radical; por eso recibe el nombre de ecuación irracional.

Ejemplo:

3·√x + 1	=	10	⟶	Comprobación
3·√x	=	10 - 1		3·√x + 1	=	10
3·√x	=	9		3·√9 + 1	=	10
(3·√x)²	=	9²		3·3 + 1	=	10
9·x	=	81		9 + 1	=	10
x	=	81		10	=	10
x	=	9
x	=	9

Ejercicio de aplicación:

Resolver cada una de las ecuaciones siguientes y comprobar el resultado:

1) √x - 8 = 2

2) 5 = √3·x + 1

3) √4·x + 5 = 5

4) 3 + √2·x = 8

5) 2·√x - 3 = -2

6) 11 = 7 + √10 - 4·x

7) 8·√x - 1 = 3

8) √7·x = 14

9) √2·x - 7 + 9 = 10

10) 2·√5·x - 3 = 7

11) √5·x + 1 = 6

12) 3·√x + 1 = 10

Autor: Hugo David Giménez Ayala. Paraguay.

Editor: Ricardo Santiago Netto (Administrador de Fisicanet).

‹ Anterior
|
Siguiente ›