Progresiones aritméticas y geométricas

1- Progresión Aritmética: es una sucesión en la cual cada término después del 1^ro se obtiene sumándole al término anterior una cantidad constante llamada razón o diferencia común.

Se la representa con el signo (:).

÷ a₁, a₂, a₃, a₄, ……………, a_n-1, a_n

Donde: a₁ = 1^er término.

a_n = último término o término general.

n = número de términos.

r = razón aritmética.

S_n = suma de los n términos.

m = n^ro de términos de los medios aritméticos.

Ley de formación

a₁
a₂ = a₁ + r		r = a₂ - a₁
a₃ = a₂ + r = (a₁ + r) + r = a₁ + 2·r
a₄ = a₃ + r = (a₁ + 2·r) + r = a₁ + 3·r	S_n =	(a₁ + a_n)_* n
		2

a_n = a₁ + (n - 1)_* r	r =	a_n - a₁
		n - 1

Interpolación de Medios Aritméticos entre 2 números dados: es formar una progresión aritmética cuyos extremos sean los 2 números dados.

÷ a₁, a₂, …………, a_n-1, a_n

m términos

Datos: a₁; a_n; n = m + 2.

Se llaman medios aritméticos a los términos de una progresión aritmética que se hallan entre el primero y el último término de la progresión.

Teorema: En toda progresión aritmética la suma de los 2 términos equidistantes de los extremos es igual a la suma de los 2 términos extremos.

Ejemplo:	÷ a₁, a₂, a₃, a₄, …………, a_n-2, a_n-1, a_n
Luego;	a₃ + a_n-2 = a₁ + a_n

Teorema: Si la progresión aritmética tiene un número impar de términos, el término medio equidista de los extremos y por tanto el doble del término medio es igual a la suma de los extremos.

Ejemplo: ÷ a₁, a₂, a₃, a₄, a₅, a₆, a₇, a₈, a₉

Luego; 2·a₅ = a₁ + a₉

2- Progresión Geométrica: es una sucesión en la cual cada término se obtiene multiplicando el anterior por una cantidad constante que es la razón o cociente común.

Se la representa con el signo (::).

:: a₁, a₂, a₃, a₄, ……………, a_n-1, a_n

Donde: a₁ = 1^er término.

a_n = último término o término general.

n = número de términos.

q = razón geométrica.

S_n = suma de los n términos.

m = n^ro de términos de los medios geométricos.

Ley de formación

a₁
a₂ = a₁·q		q = a₂/a₁
a₃ = a₂·q = (a₁·q)·q = a₁·q²
a₄ = a₃·q = (a₁·q²)·q = a₁·q³	S_n =	a₁·(qⁿ - 1)
		q - 1

a_n = a₁*q^{(n - 1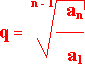)}	n =		log a_n - log a₁	+ 1
			log q

Interpolación de Medios Geométricos entre 2 números dados: es formar una progresión geométrica cuyos extremos sean los 2 números dados.

:: a₁, a₂, …………, a_n-1, a_n

m términos

Datos: a₁; a_n; n = m + 2.

Se llaman medios geométricos a los términos de una progresión geométrica que se hallan entre el primero y el último término de la progresión.

Teorema:

En toda progresión geométrica el producto de los 2 términos equidistantes de los extremos es igual al producto de los 2 términos extremos.

Ejemplo: a₁, a₂, a₃, a₄, …………, a_n-2, a_n-1, a_n

Luego; a_3* a_n-2 = a_1* a_n

Teorema:

Si la progresión geométrica tiene un número impar de términos, el cuadrado del término medio equivale al producto de los extremos.

Ejemplo: a₁, a₂, a₃, a₄, a₅, a₆, a₇, a₈, a₉

Luego; (a₅)² = a_1* a₉

3) Resolver los siguientes ejercicios:

1) Hallar el 9^no término de una progresión aritmética: (7, 10, 13, …………).

2) Calcular el 21° término de una progresión aritmética (P.A.) (-⅗, -14/15, ……………).

3) Determinar el término general de la progresión aritmética: (6, 9, ………).

4) Hallar el 39° término de una progresión aritmética (P.A.) (-3, -5/4, …………).

5) Encontrar el término general de la progresión aritmética (P.A.) (x - 1, x, ………).

6) Hallar el 19° término de una progresión aritmética (P.A.) (⅚, -⅓, ………).

7) Hallar el 9^no término de la progresión aritmética (P.A.) (1, 6, 11, ……………).

8) El 15° término de una progresión aritmética (P.A.) es 20 y la razón es 2/7. Hallar el 1^er término.

9) Calcular la razón de una progresión aritmética (P.A.) (3, ………, 8, …); donde 8 es el 6^to término.

10) Cuántos términos tiene la progresión aritmética (P.A.) (4, 6, …………, 30).

11) Determinar el 1^er término de la progresión aritmética (P.A.) en que el 15° término es 44 y la razón es 3.

12) En una progresión aritmética (P.A.) el 1^er término es 5 y la razón es 9. Determinar el orden del término igual a 239.

13) El 5^to término de una progresión aritmética (P.A.) es 7 y el 7^mo término es 25/3. Hallar la razón.

14) Una progresión aritmética (P.A.) comienza por 2, termina con 3 y su razón es ⅒. Cuántos términos hay en la progresión.

15) El 1^er término de una progresión aritmética es 23 y el último es 35. Determinar la progresión sabiendo que el número de términos es igual a la razón.

16) Sí el 31° término de una progresión aritmética (P.A.) es 156 y el 1^er término es 6; determínese la razón de la misma.

17) Hallar la suma de la progresión aritmética: (0,2; 0,7; 1,2; ………………); siendo n = 12.

18) la suma de 3 números que están en progresión aritmética (P.A.) es 21 y el producto de los mismos es 231. Calcular esos números.

19) Hallar 3 números en progresión aritmética (P.A.) cuya suma es 54 y cuyo producto es 5.670.

20) la suma de 3 números que están en progresión aritmética es 9 y la suma de sus cuadrados es 35. Hallar los 3 números.

21) Cuántos múltiplos de 5 existen entre el 18 y el 193.

22) Cuántos múltiplos de 11 existen entre 100 y 1.000.

23) Hallar la suma de los 8 primeros términos de una progresión aritmética (P.A.) (15, 19, 23, ……………).

24) Hallar la suma de los 72 primeros múltiplos de 11 que siguen a 76.

25) Hallar la suma de los 43 primeros números terminados en 9.

26) Hallar la suma de los 20 primeros múltiplos de 7.

27) Hallar la suma de los 80 primeros múltiplos de 5.

28) Hallar la suma de los impares del 51 al 813.

29) Hallar la suma de los 100 primeros números pares.

30) Hallar la suma de los 100 primeros números impares mayores que 7.

31) Interpolar 3 medios aritméticos entre -1 y 7.

32) Interpolar 3 medios aritméticos entre 3 y 11.

33) Interpolar 4 medios aritméticos entre 8 y 23.

34) Interpolar 4 medios aritméticos entre -42 y 53.

35) Interpolar 4 medios aritméticos entre 1 y 3.

36) Interpolar 5 medios aritméticos entre -6 y 18.

37) Interpolar 6 medios aritméticos entre 1 y ½.

38) Interpolar 9 medios aritméticos entre 18 y -12.

39) Hallar el 5^to término de una progresión geométrica (P.G.) (⅚, ½, ……………).

40) Encontrar el 9^no término de la progresión geométrica :: (2, 8, …………).

41) Calcular 9^no término de la progresión geométrica (P.G.) (1/32, 1/16, ⅛, ………………).

42) Hallar el 10^mo término de una progresión geométrica (P.G.) (-¾, -¼, -1/12, ………).

43) Hallar el 11° término de una progresión geométrica (progresión geométrica (P.G.)) (-8, -4, -2, …………).

44) Determinar el 15° término de la progresión geométrica :: (2, 6, …………).

45) Determinar el término general (a_n) de la progresión geométrica :: (5, 25, 125, …………).

46) Hallar el número de términos de una progresión geométrica (P.G.) (4, 8, ……………, 512).

47) Hallar el 1^er término de una progresión geométrica (P.G.) de razón 2; siendo el 10^mo término igual a 1.536.

48) El 9^no término de una progresión geométrica (P.G.) es 64/2.187 y su razón es ⅔. Hallar el 1^er término.

49) El 4^to término de una progresión geométrica (P.G.) es ¼ y el 7^mo término es 1/32. Hallar el 6^to término.

50) El 3^er término de una progresión geométrica (P.G.) es 28 y el 5^to término es 112. Formar la progresión.

51) la razón de una progresión geométrica es ½ y el 7^mo término es 1/64. Hallar el 1^er término.

52) En una progresión geométrica (P.G.), el 2^do término es igual a 6 y el 5^to término es 2/9. Formar la progresión.

53) En una progresión geométrica (P.G.), el 1^er término es 3 y la razón es 4. Determinar el orden del término igual a 768.

54) la razón de una progresión geométrica de 5 términos es 4 y el último término es 1.280. ¿Cuál es el 1^er término de dicha progresión?

55) En una progresión geométrica (P.G.) de 4 términos, el 1^er término es 12 y el último término es 96. Calcular la razón y formar la progresión.

56) En una progresión geométrica (P.G.) de razón - 5 el 1^er término es 25 y el último es -3.125. Determinar el número de términos de está progresión.

57) En una progresión geométrica de 5 términos el cuadrado del 3^er término es 4/81. Sí el último término es 8/81. Cuál es el primero.

58) Calcular la suma de los términos de la progresión geométrica :: (3, 6, …………, 2.187).

59) Hallar la suma de los 5 primeros términos de una progresión geométrica (P.G.) (6, 3, 3/2, ……………).

60) Hallar la suma de los 7 primeros términos de una progresión geométrica (P.G.) (-⅒, ⅕, -⅖, …………).

61) Calcular la suma de los primeros 8 términos de la progresión geométrica (P.G.) (1, ½, ¼, ……………).

62) Calcular la suma de los 9 primeros términos de la progresión geométrica (P.G.) (2, 6, 18, ………………).

63) En una progresión geométrica la suma de los términos es 510. Sabiendo que el último término es 256 y la razón es 2. Calcular el 1^er término.

64) El 1^er término de una progresión geométrica (P.G.) es 375 y el 4^to término es 192. Calcular la razón y la suma de los cuatro primeros términos.

65) Interpolar 3 medios geométricos entre 1 y 81.

66) Interpolar 4 medios geométricos entre -7 y -224.

67) Interpolar 4 medios geométricos entre 2 y 486.

68) Interpolar 4 medios geométricos entre 4/9 y 27/256.

69) Interpolar 5 medios geométricos entre 32/81 y 9/2.

70) Interpolar 6 medios geométricos entre 512 y -4.

4) Resolver los siguientes problemas:

1) Las sumas del 1^er y 3^er término de una progresión aritmética es 12; y las sumas del 2^do y 5^to término es 21. Hallar los términos y la razón.

2) El 3^er y 5^to término de una progresión aritmética (P.A.) suman 46; y el 4^to y 6^to término suman 58. Hallar la razón y el valor de dichos términos.

3) El 2^do y 4^to término de una progresión aritmética (P.A.) suman 22; y el 3^er y 6^to término suman 34. Hallar el valor de las incógnitas.

4) El 4^to y 3^er término de una progresión aritmética (P.A.) suman 2; y el 3^er con el 5^to término suman 4. Hallar las incógnitas.

5) la suma del 2^do y 3^er término de una progresión aritmética es -5 y la suma del 5^to y 6^to término es 13. Hallar la razón y el valor de dichos términos.

6) Las ganancias de 3 años de una empresa están en progresión aritmética. El 1^er año ganó 10.000 $ y el 3^er año 24.000 $. Cuál fue la ganancia del 2^do año.

7) En el 1^er mes de negocios una persona ganó 500 $ y en el último ganó 1.900 $. Sí en cada mes ganó 200 $ más que el mes anterior. ¿Cuántos meses tuvo el negocio?

8) Se compra 1 artículo a pagar en 15 meses de este modo: 1 $ el 1^er mes; 3 $ el 2^do mes; 9 $ el 3^er mes y así sucesivamente. Cuál es el importe del artículo.

9) Un hombre avanza en el 1^er segundo de su carrera 6 m y en cada segundo posterior avanza 25 cm más que el anterior. Cuánto avanzó en el 8^vo segundo y qué distancia habrá recorrido en ese tiempo.

10) Hallar las longitudes de los lados de un triángulo, sabiendo que están en progresión aritmética de razón igual a 6 cm y que su perímetro es igual a 54 cm.

11) Una deuda debe ser pagada en 32 semanas; pagando 5 $ la 1^ra semana, 8 $ la 2^da semana, 11 $ la 3^ra semana y así sucesivamente. Hallar el importe de la suma.

12) Los ahorros de los 3 primeros meses de una familia están en progresión aritmética (P.A.) Sí en los 3 meses ha ahorrado 2.400 $ y el 1^er mes ahorró la mitad de lo que ahorró el 2^do mes. Cuánto ahorró cada mes.

13) El perímetro de un triángulo rectángulo es 60 cm. Calcular las longitudes de los lados, sabiendo que están en progresión aritmética.

14) Una piedra dejada caer libremente desde la azotea de un edificio recorre 16,1 pies en el 1^er segundo y en cada segundo posterior recorre 32,2 pies más que el 2^do anterior. Sí la piedra tarda 5 segundos en llegar al suelo. Cuál es la altura del edificio.

15) Calcular las longitudes de los lados de un triángulo rectángulo, sabiendo que sus medidas expresadas en cm son números que están en progresión aritmética (P.A.) cuya razón es igual a 7.

16) Las ganancias mensuales de un comerciante durante 11 meses están en progresión aritmética. El 1^er mes ganó 1.180 $ y el último 6.180 $. Cuánto más ganó en cada mes a contar del 2^do mes, que en el anterior.

17) Determinar las longitudes de los lados de un triángulo rectángulo, sabiendo que están en progresión aritmética (P.A.) de razón igual a 5.

18) Determinar el valor de x para que formen progresión aritmética de x², (x + 2)², (x + 3)²

19) Determinar el valor de x para que formen progresión aritmética (P.A.) de (3·x - 1), (x + 3), (x + 9).

20) En una progresión geométrica de razón positiva, la suma del 3^er término con el 4^to es 240 y la suma del 5^to con el 6^to es 3.840. Calcular la razón y formar la progresión.

21) Calcular la razón de una progresión geométrica (P.G.) de 5 términos; sabiendo que la suma de los dos primeros términos es 120 y la suma de los dos últimos es 960.

22) Una progresión geométrica (P.G.) de razón positiva consta de 4 términos. Sabiendo que la suma de los dos primeros es 6 y que la correspondiente de los dos últimos es 24, determinar la razón y formar la progresión.

23) El valor del 3^er término de una progresión geométrica es 32 y la diferencia entre el 4^to y el 2^do término es 120. Calcular la razón y la suma de los 4 primeros términos.

24) ¿Cuántos términos debemos considerar en la progresión geométrica (P.G.) (3, 6, ………) para obtener una suma de 1.533?

25) la suma de 3 números consecutivos que están en progresión geométrica es 28 y el producto entre ellos es 512. Calcular los 3 números.

26) la suma de los tres primeros términos de una progresión geométrica (P.G.) es 77 y su producto es 10.648. Calcular los tres números.

27) la suma de 3 números positivos en una progresión geométrica es 210, el tercero excede al primero en 90. Hallar los 3 números positivos.

28) Hallar 3 números que están en progresión geométrica (P.G.), sabiendo que su suma es 65 y su producto es 3.375.

29) Hallar el valor de x para que la sucesión (2·x - 5), (x - 4), (10 - 3·x) sea una progresión geométrica (P.G.)

30) Hallar el valor de x para que la sucesión x, (x + 9), (x + 45) sea una progresión geométrica (P.G.)

31) Hallar el valor de x, de modo que los números (x - 5), x, (x + 10); en ese orden, estén en progresión geométrica (P.G.) Construir dicha progresión.

Autor: Hugo David Giménez Ayala. Paraguay.

Editor: Ricardo Santiago Netto (Administrador de Fisicanet)