Operaciones con matrices

Suma y resta de matrices

Para poder sumar o restar matrices, éstas deben tener el mismo número de filas y de columnas. Es decir, si una matriz es de orden 3× 2 y otra de 3×3, no se pueden sumar ni restar. Esto es así ya que, tanto para la suma como para la resta, se suman o se restan los términos que ocupan el mismo lugar en las matrices.

Ejemplos de suma y resta de matrices

Sean las matrices:

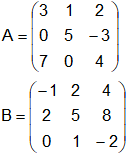
Entonces:

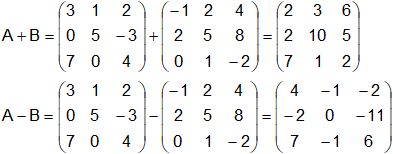
Para sumar o restar más de dos matrices se procede igual. No necesariamente para poder sumar o restar matrices, éstas tienen que ser cuadradas.

Ejemplo:

Sean

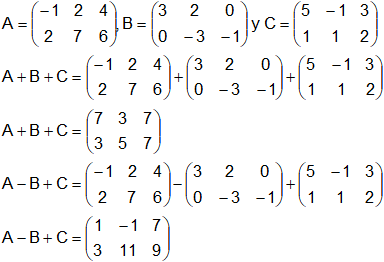
Producto de matrices

Para poder multiplicar dos matrices, la primera debe tener el mismo número de columnas que filas la segunda. La matriz resultante del producto quedará con el mismo número de filas de la primera y con el mismo número de columnas de la segunda. Es decir, si tenemos una matriz 2×3 y la multiplicamos por otra de orden 3×5, la matriz resultante será de orden 2×5.

(2×3)×(3×5) = (2×5)

Se puede observar que el producto de matrices no cumple la propiedad conmutativa, ya que en el ejemplo anterior, si multiplicamos la segunda por la primera, no podríamos efectuar la operación.

3×5 por 2×3,

Puesto que la primera matriz no tiene el mismo número de columnas que filas la segunda. Supongamos que A = (aₓ) y B = (bₓ) son matrices tales que el número de columnas de A coincide con el número de filas de B; es decir, A es una matriz m×p y B una matriz p×n. Entonces el producto AB es la matriz m×n cuya entrada ij se obtiene multiplicando la fila i de A por la columna j de B. Esto es,

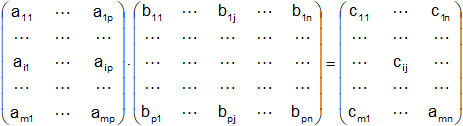
Donde c_ij = aᵢ₁ b_1j + aᵢ₂ b_2j + … + aᵢₚ b_pj

Ejemplo:

1.

2.

Producto por un escalar

El producto de un escalar k por la matriz A, escrito k·A o simplemente k·A, es la matriz obtenida multiplicando cada entrada de A por k:

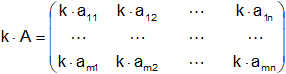
Ejemplo:

Sea

Entonces:

División de matrices

La división de matrices se define como el producto del numerador multiplicado por la matriz inversa del denominador. Es decir, sean las matrices A y B tal que A/B = AB⁻¹:

Si una matriz está dividida entre un escalar, todos los términos de la matriz quedarán divididos por ese escalar.

Ejemplo:

Sean la matriz , y k = 2 un escalar.

En este caso:

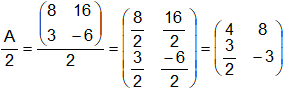
Autor: Jesús. España.

Editor: Ricardo Santiago Netto (Administrador de Fisicanet).

• ‹ Anterior
• |
• Siguiente ›