Matrices invertibles

Se dice que una matriz cuadrada A es invertible, si existe una matriz B con la propiedad de que

AB = BA = I

Siendo I la matriz identidad. Denominamos a la matriz B la inversa de A y la denotamos por A^-1

Ejemplo:

Supongamos A =		2	5
		1	3

y B =		3	-5
		-1	2

Entonces:

A·B =		2	5		·		3	-5		=		6 - 5		-10 + 10		=		1	0		= I
		1	3				-1	2				3 - 3		-5 + 6				0	1

A·B =		3	-5		·		2	5		=		6 - 5		15 - 15		=		1	0		= I
		-1	2				1	3				-2 + 2		-5 + 6				0	1

Puesto que AB = BA = I, A y B son invertibles, siendo cada una la inversa de la otra.

Método de Gauss

Sea A = (a_x) una matriz cuadrada de orden n. Para calcular la matriz inversa de A, que denotaremos como A^-1, seguiremos los siguientes pasos:

Paso 1. Construir la matriz n×2·n M = (A ⋮ I) esto es, A está en la mitad izquierda de M y la matriz identidad I en la derecha.

Paso 2. Se deja tal y como está la primera fila de M, y debajo del primer término de la diagonal principal, a₁₁, que llamaremos pivote, ponemos ceros. Luego se opera como se indica en el siguiente ejemplo.

Ejemplo:

Consideremos una matriz 3×3 arbitraria.

A =	a₁₁	a₁₂	a₁₃
	a₂₁	a₂₂	a₂₃
	a₃₁	a₃₂	a₃₃

Paso 1

M = (A ⋮ I) =	a₁₁	a₁₂	a₁₃	⋮	1	0	0	~
	a₂₁	a₂₂	a₂₃	⋮	0	1	0
	a₃₁	a₃₂	a₃₃	⋮	0	0	1

Paso 2

a₁₁

a₁₂

a₁₃

⋮

a₁₁·a₂₂ - a₂₁·a₁₂

a₁₁·a₂₃ - a₂₁·a₁₃

⋮

a₁₁·0 - a₂₁·1

a₁₁·1 - a₂₁·0

a₁₁·0 - a₂₁·0

a₁₁·a₃₂ - a₃₁·a₁₂

a₁₁·a₃₃ - a₃₁·a₁₃

⋮

a₁₁·1 - a₃₁·1

a₁₁·0 - a₃₁·0

a₁₁·1 - a₃₁·0

El siguiente paso es igual que el anterior, pero esta vez se coge como pivote el segundo término de la diagonal principal. Al llegar al último término de la diagonal, se procede igual que antes, pero poniendo los ceros encima del nuevo pivote. Se observa que al coger como pivote el último término de la diagonal, la matriz A se transforma en una matriz triangular.

Una vez realizados todos los pasos, la mitad izquierda de la matriz M se convierte en una matriz diagonal. En este momento hay que proceder a transformar, si es que no lo está, la mitad izquierda en la matriz identidad, dividiendo si fuera necesario las filas de M por un escalar.

Ejemplo: Supongamos que queremos encontrar la inversa de

A =	1	0	2
	2	-1	3
	4	1	8

Primero construimos la matriz M = (A ⋮ I),

M =	1	0	2	⋮	1	0	0
	2	-1	3	⋮	0	1	0
	4	1	8	⋮	0	0	1

~	1	0	2	⋮	1	0	0	~
	0	-1 - 2,0	3 - 2,2	⋮	0 - 2	1 - 2,0	0
	0	1 - 4,0	8 - 4,2	⋮	0 - 4	0	1 - 0

~	1	0	2	⋮	1	0	0
	0	-1	-1	⋮	-2	1	0
	0	1	0	⋮	-4	0	1

Luego se toma como pivote a₂₂ = -1,

~	1	0	2	⋮	1	0	0	~
	0	-1	-1	⋮	-2	1	0
	0	0	0 - (-1)	⋮	4 - (-2)	0 - 1	-1 - 0

~	1	0	2	⋮	1	0	0	~
	0	-1	-1	⋮	-2	1	0
	0	0	1	⋮	6	-1	-1

La mitad izquierda de M está en forma triangular, por consiguiente, A es invertible. Si hubiera quedado toda una fila con ceros en la mitad A de M, la operación habría terminado (A no es invertible). A continuación, cogemos como pivote a₃₃, ponemos ceros encima de éste y seguimos operando hasta que nos quede una matriz diagonal.

~	1	0	0	⋮	-11	2	2
	0	-1	0	⋮	4	0	1
	0	0	1	⋮	6	-1	-1

Ya que la matriz colocada en la mitad izquierda es diagonal, no hay que operar más. Transformamos la matriz diagonal en una matriz identidad; para ello hay que dividir la segunda fila entre -1:

~	1	0	0	⋮	-11	2	2
	0	1	0	⋮	-4	0	1
	0	0	1	⋮	6	-1	-1

La matriz que ha quedado en la mitad derecha de M es precisamente la matriz inversa de A:

A^-1 =	-11	2	2
	-4	0	1
	6	-1	-1

Para comprobar si el resultado es correcto, se procede a multiplicar AA^-1, teniendo que dar como resultado la matriz identidad I.

Comprobación:

AA^-1 = I

1	0	2	·	-11	2	2	=
2	-1	3		-4	0	1
4	1	8		6	-1	-1

=	-11 + 0 + 12	2 + 0 - 2	2 + 0 - 2	=	1	0	0	= I
	-22 + 4 + 18	4 + 0 - 3	4 - 1 - 3		0	1	0
	-44 - 4 + 48	8 + 0 - 8	8 + 1 - 8		0	0	1

Ejemplo de operaciones con matrices

Ejemplo n° 1

Sean

A =	2	4	1
	1	-2	3
	5	0	-1

B =	3	-1	-2
	0	5	6
	0	0	9

C =	2	0	1
	0	-1	2
	1	-2	5

1) ¿Qué clase de matrices son?

2) Calcular:

-A - B + C.

A + B - C

3·A + C/2

3) Calcular:

(A·B)/C

4) Calcular la inversa de A (A^-1) y comprobar el resultado.

Solución

Las tres matrices son cuadradas y de orden tres. A su vez, B es una matriz triangular, ya que todas las entradas debajo de la diagonal principal son ceros, y C es antisimétrica porque los elementos simétricos son opuestos entre sí.

-A - B + C = -	2	4	1	-	3	-1	-2	+	2	0	1	=
	1	-2	3		0	5	6		0	-1	2
	5	0	-1		0	0	9		1	-2	5

=	-2 - 3 + 2	-4 + 1 + 0	-1 + 2 - 1	=	-3	-3	0
	-1 - 0 + 0	2 - 5 - 1	-3 - 6 + 2		-1	-4	-7
	-5 - 0 + 1	0 - 0 - 2	1 - 9 + 5		-4	-2	-3

A + B - C =	2	4	1	+	3	-1	-2	-	2	0	1	=
	1	-2	3		0	5	6		0	-1	2
	5	0	-1		0	0	9		1	-2	5

=	2 + 3 - 2	4 - 1 - 0	1 - 2 + 1	=	3	3	0
	1 + 0 - 0	2 + 5 + 1	3 + 6 - 2		1	4	7
	5 - 0 - 1	0 + 0 + 2	-1 + 9 - 5		4	2	3

						2	0	-1
						0	-1	2
3·A + C/2 = 3·	2	4	1	+		1	-2	5	=

	1	-2	3		2
	5	0	-1

=	6	12	3	+	1	0	-½	=
	3	-6	9		0	-½	1
	15	0	-3		½	-1	5/2

6 + 1

12 + 0

3 - ½

5/2

3 + 0

-6 - ½

9 + 1

-13/2

15 + ½

0 - 1

-3 + 5/2

31/2

-1

-1/2

Puesto que (A·B)/C = A·B·C^-1, calcularemos primero la inversa de C y luego haremos el producto.

C^-1 =	2	0	-1	⋮	1	0	0
	0	-1	2	⋮	0	1	0
	1	-2	5	⋮	0	0	1

~	2	0	-1	⋮	1	0	0	~
	0	-1	2	⋮	0	1	0
	0	-4	11	⋮	-1	0	2

~	2	0	-1	⋮	1	0	0	~
	0	-1	2	⋮	0	1	0
	0	0	-3	⋮	1	4	-2

~	-6	0	0	⋮	-2	4	-2	~
	0	3	0	⋮	-2	-11	4
	0	0	-3	⋮	1	4	-2

Dividimos la primera fila entre -6, la segunda entre 3 y la tercera entre -3 para que en la mitad izquierda quede la matriz identidad,

~	1	0	0	⋮	-⅓	-⅔	⅓
	0	1	0	⋮	-⅔	-11/3	4/3
	0	0	1	⋮	-⅓	-4/3	⅔

Por lo tanto, la matriz inversa de C es:

C^-1 =	-⅓	-⅔	⅓
	-⅔	-11/3	4/3
	-⅓	-4/3	⅔

A continuación, se calcula el producto de las matrices A y B,

A·B =	2	4	1	·	3	-1	-2	=	6	18	29	,
	1	-2	3		0	5	6		3	-11	13
	5	0	-1		0	0	9		15	-5	-19

Por último, calculamos (A·B)·C^-1

(A·B)·C^-1 =	6	18	29	·	1/3	-2/3	1/3	=
	3	-11	13		-2/3	-11/3	4/3
	15	-5	-19		-1/3	-4/3	2/3

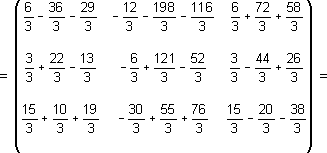
Ejemplo del producto de matrices

(A·B)·C^-1 =	59/3	326/3	136/3
	4	21	-5
	44/3	101/3	-43/3

Sacando factor común ⅓, el resultado puede escribirse como:

(A·B)·C^-1 = ⅓·	59	326	136
	12	63	-15
	44	101	-43

Primero se construye la matriz M = (A ⋮ I) y luego se va desarrollando por Gauss. Así pues:

M = (A ⋮ I) =	2	4	1	⋮	1	0	0	~
	1	-2	3	⋮	0	1	0
	5	0	-1	⋮	0	0	1

~	2	4	1	⋮	1	0	0	~
	0	-8	5	⋮	-1	2	0
	0	0	156	⋮	-5	0	2

~	2	4	1	⋮	1	0	0	~
	0	-8	5	⋮	-1	2	0
	0	0	39	⋮	20	40	-16

Se simplifica un poco para que las operaciones no sean tan costosas, dividiendo la tercera fila entre cuatro. De este modo, se tiene

~	2	4	1	⋮	1	0	0	~
	0	-8	5	⋮	-1	2	0
	0	0	39	⋮	5	10	-4

y se contínua calculando,

~	78	156	0	⋮	34	-10	4	~
	0	-312	0	⋮	-64	28	20
	0	0	39	⋮	5	10	-4

Se vuelve a simplificar, dividiendo la primera fila entre dos y la segunda entre cuatro,

~	39	78	0	⋮	17	-5	2	~
	0	-78	0	⋮	-16	7	5
	0	0	39	⋮	5	10	-4

~	-3.042	0	0	⋮	-78	-156	-546	~
	0	-78	0	⋮	-16	7	5
	0	0	39	⋮	5	10	-4

Puesto que ya ha quedado una matriz diagonal en la mitad izquierda de M, se procede a transformar esta mitad izquierda en una matriz identidad, dividiendo la primera fila entre -3.042, la segunda entre -78 y la tercera entre 39,

~	1	0	0	⋮	1/39	2/39	7/39	~
	0	1	0	⋮	8/39	-7/78	-5/78
	0	0	1	⋮	5/39	10/39	-4/39

Así pues, la matriz que ha quedado en la mitad derecha es precisamente la matriz identidad, que sacando factor común 1/78 se puede escribir como:

A^-1 = (1/78)·	2	4	14
	16	-7	-5
	10	20	-8

Para comprobar el resultado, la matriz inversa de A o A^-1, tiene que cumplir

A·A^-1 = I.

Procedamos a la comprobación:

A·A^-1 =	2	4	1	·	2	4	14	·1/78 =
	1	-2	3		16	-7	-5
	5	0	-1		10	20	-8

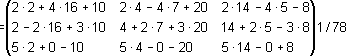
Ejemplo de cálculo de la inversa de una matriz

A·A^-1 =	78	0	0	·1/78 =	1	0	0	= I
	0	78	0		0	1	0
	0	0	78		0	0	1

‹ Anterior
|
Siguiente ›

Autor: Jesús

España.

Editor: Ricardo Santiago Netto (Administrador de Fisicanet)

Ver condiciones para uso de los contenidos de fisicanet.com.ar

🔍
✉ f t