Propiedades de los determinantes
Las propiedades básicas del determinante son las siguientes:
1) El determinante de una matriz A y el de su traspuesta AT son iguales, es decir,
- |A| = |AT|
2) Sea A una matriz cuadrada,
- Si A posee dos filas (columnas) iguales, necesariamente |A| = 0
- Si A es triangular, esto es, A sólo tiene ceros por encima o por debajo de la diagonal principal, entonces |A| es igual al producto de los elementos de la diagonal
3) Supongamos que B se ha obtenido de A mediante una operación elemental entre filas o columnas,
- Si se han intercambiado dos filas (columnas) de A, |B| = -|A|
- Si se ha sumado un múltiplo de una fila (columna) a otra, entonces |B| = |A|
- Si se ha multiplicado una fila (columna) de A por un escalar k, |B| = k·|A|
4) Sea A cualquier matriz n-cuadrada, son equivalentes los siguientes principios:
- A es invertible, es decir, A tiene inversa A⁻¹
- AX = 0 tiene solamente la solución trivial
- El determinante de A no es nulo: |A| ≠ 0
5) El determinante es una función multiplicativa. Es decir, el determinante del producto de matrices A y B es el producto de los determinantes: |A·B| = |A|·|B|
6) Supongamos que A y B son matrices similares, entonces: |A| = |B|
Determinante de orden arbitrario
Sea A = (aₙₙ) una matriz de orden arbitrario n·n (siendo n un número par). Para calcular el det (A) se procede de la siguiente manera:

Los signos se van alternando según la posición que ocupen las entradas del determinante. Es decir:
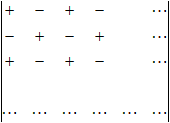
Ejemplo:
Calcular el determinante de:

Si observamos la matriz, podemos ver que en la tercera columna hay dos ceros. Así pues, si cogemos las entradas de la tercera columna para calcular el determinante, nos ahorraremos calcular dos determinantes, ya que el producto de un determinante por cero es cero.
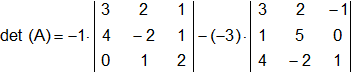
det (A) = -1·(-12 + 0 - 4 - 16 - 3) + 3·(15 + 0 + 2 + 20 - 2 - 0) =
det (A) = -1·(-35) + 3·(35) = 35 + 105 = 140
Ejemplo de cálculo de determinantes
Ejemplo nº 1
Calcular los siguientes determinantes:
a)
![]()
b)
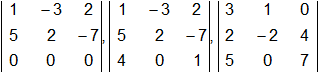
c)

a)
![]() = 5 - (-6) = 5 + 6 = 11
= 5 - (-6) = 5 + 6 = 11
![]() = -12 - (-2) = -12 + 2 = -10
= -12 - (-2) = -12 + 2 = -10
b)
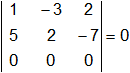
Al haber toda una fila nula, el determinante da como resultado = 0.
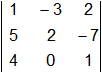 = 2 + 48 + 0 - 16 - (-15) - 0 =
= 2 + 48 + 0 - 16 - (-15) - 0 =
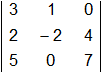 = -42 + 20 + 0 - 0 - 14 - 0 = -36
= -42 + 20 + 0 - 0 - 14 - 0 = -36
c)
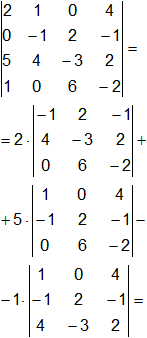
= 2·(-6 - 24 + 16 + 2) + 5·(-4 - 24 + 6) - 1·(4 + 12 - 16 - 3) = -24 - 110 + 3 = -131

= 1·[16 + 0 + 24 - (-4) - (-30) - 0] - 2·[-128 - 2 + 30 - (-40) - 12 - (-16)] = 74 - 2·(-56) = 74 + 112 = 186
Autor: Jesús. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
¿Qué es un sistema de ecuaciones lineales de 3x3? ¿Qué son los determinantes en matemáticas?