Determinantes
A cada matriz n-cuadrada A = (aij) se le asigna un escalar particular denominado determinante de A, denotado por det (A), | A | o
| a₁₁ | a₁₂ | … | a₁ₙ |
| a₂₁ | a₂₂ | … | a₂.ₙ |
| … | … | … | … |
| aₘ₁ | aₘ₂ | … | aₘₙ |
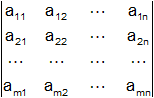
Una tabla ordenada n×n de escalares situada entre dos líneas verticales, llamada determinante de orden n, no es una matriz. La función determinante apareció por primera vez en el estudio de los sistemas de ecuaciones lineales. Veremos que es una herramienta indispensable en el estudio y obtención de éstas.
Determinantes de orden uno y dos
Los determinantes de orden uno y dos se definen como sigue:
|a₁₁| = a₁₁
| a₁₁ | a₁₂ | = a₁₁·a₂₂ - a₁₂·a₂₁ |
| a₂₁ | a₂₂ |
Así, el determinante de una matriz 1. 1 A = (a₁₁) es el propio escalar a₁₁, es decir, det (A) = |a₁₁| = a₁₁
Ejemplos:
a)
Dado que el determinante de orden uno es el mismo escalar, tenemos det (24) = 24, det(-3) = -3, det (3·x + 5) = 3·x + 5.
b)
| 3 | 5 | = (3)·(1) - (5)·(2) = 3 - 10 = -7 |
| 2 | 1 |
| 2 | -3 | = (2)·(-4) - (-3)·(1) = -8 - (-3) = -8 + 3 = -5 |
| 1 | -4 |
Determinantes de orden tres
Consideremos una matriz 3×3 arbitraria A = (aij). El determinante de A se define como sigue:
| det (A) = | a₁₁ | a₁₂ | a₁₃ | = |
| a₂₁ | a₂₂ | a₂₃ | ||
| a₃₁ | a₃₂ | a₃₃ |
= a₁₁·a₂₂·a₃₃ + a₁₂·a₂₃·a₃₁ + a₂₁·a₃₂·a₁₃ - a₁₃·a₂₂·a₃₁ - a₁₂·a₂₁·a₃₃ - a₃₂·a₂₃·a₁₁
Obsérvese que hay seis productos, cada uno formado por tres elementos de la matriz. Tres de los productos aparecen con signo positivo (conservan su signo) y tres con signo negativo (cambian su signo). Para calcular los determinantes de orden tres, el siguiente diagrama puede ayudar a resolverlos:
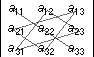(Para los tres productos positivos)
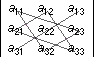(Para los tres productos negativos)
Ejemplo: Calcular el valor del determinante:
| 3 | 2 | 1 | = |
| 0 | 2 | -5 | |
| -2 | 1 | 4 |
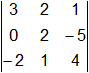= (3)·(2)·(4) + (2)·(-5)·(-2) + (0)·(1)·(1) - (-2)·(2)·(1) - (0)·(2)·(4) - (1)·(-5)·(3) =
= 24 + 20 + 0 - (-4) - 0 - (-15) = 44 + 4 + 15 = 63
El determinante de la matriz 3×3 A = (aₓ) puede reescribirse como:
det (A) = a₁₁(a₂₂a₃₃ - a₂₃a₃₂) - a₁₂(a₂₁a₃₃ - a₂₃a₃₁) + a₁₃(a₂₁a₃₂ - a₂₂a₃₁) =
| = a₁₁ | a₂₂ | a₂₃ | - a₁₂ | a₂₁ | a₂₃ | + a₁₃ | a₂₁ | a₂₂ |
| a₃₂ | a₃₃ | a₃₁ | a₃₃ | a₃₁ | a₃₂ |
Que es una combinación lineal de tres determinantes de orden dos, cuyos coeficientes (con signos alternantes) constituyen la primera fila de la matriz dada. Esta combinación lineal puede indicarse de la forma siguiente:
| a₁₁ | a₁₁ | a₁₂ | a₁₃ | - a₁₂ | a₁₁ | a₁₂ | a₁₃ | + a₁₃ | a₁₁ | a₁₂ | a₁₃ |
| a₂₁ | a₂₂ | a₂₃ | a₂₁ | a₂₂ | a₂₃ | a₂₁ | a₂₂ | a₂₃ | |||
| a₃₁ | a₃₂ | a₃₃ | a₃₁ | a₃₂ | a₃₃ | a₃₁ | a₃₂ | a₃₃ |
Nótese que cada matriz 2×2 se obtiene suprimiendo en la matriz inicial la fila y la columna que contienen su coeficiente.
Ejemplo:
Para demostrar que la propiedad anterior se cumple, trabajaremos con:
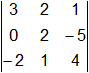| 3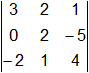 | 2 | 1 | = |
| 0 | 2 | -5 | |
| -2 | 1 | 4 |
| = 3· | 3 | 2 | 1 | - 2· | 3 | 2 | 1 | + 1· | 3 | 2 | 1 | = |
| 0 | 2 | -5 | 0 | 2 | -5 | 0 | 2 | -5 | ||||
| -2 | 1 | 4 | -2 | 1 | 4 | -2 | 1 | 4 |
| = 3· | 2 | -5 | - 2· | 0 | -5 | + 1· | 0 | 2 | = |
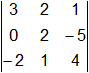| 1 | 4 | -2 | 4 | -2 | 1 |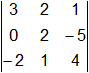
= 3·(8 + 5) - 2·(0 - 10) + 1·(0 + 4) = 39 + 20 + 4 = 63
Autor: Jesús. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
¿Qué es un sistema de ecuaciones lineales de 3x3? ¿Qué son los determinantes en matemáticas?