Problema nº 1-j de sistemas de ecuaciones con dos incágnitas, lineales - TP01
Enunciado del ejercicio nº 1-j
Resolver el siguiente sistema de ecuaciones lineales por los métodos de:
I) Igualación
II) Sustitución
III) Reducción
IV) Determinantes
V) Graficar
x + 2·y = 0
5·x + 10·y = 14
Solución
I) Igualación
x + 2·y = 0
5·x + 10·y = 14
Despejamos "y" en ambas ecuaciones:
| y = | -x |
| 2 |
| y = | -5·x + 14 |
| 10 |
Igualamos y resolvemos:
| -x | = | -5·x + 14 |
| 2 | 10 |
10·(-x) = 2·(-5·x + 14)
-5·x = -5·x + 14
Despejamos "x":
-5·x + 5·x = 14
0 = 14 ∉
Resultado, el sistema no tiene solución.
II) Sustitución
x + 2·y = 0
5·x + 10·y = 14
Se omite la resolución por este método, el sistema no tiene solución.
III) Reducción
x + 2·y = 0
5·x + 10·y = 14
Se omite la resolución por este método, el sistema no tiene solución.
IV) Determinantes
x + 2·y = 0
5·x + 10·y = 14
Se omite la resolución por este método, el sistema no tiene solución.
• Verificar que el determinante del sistema (determinante de los coeficientes) sea nulo.
Las rectas no se intersecan.
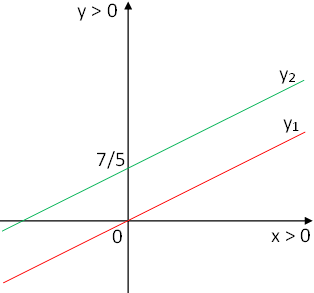
V) Gráfica
Despejamos "y" de ambas ecuaciones para obtener la ordenada al origen (b) y la pendiente (m) de las rectas:
| y = | -x |
| 2 |
| m₁ = - | 1 |
| 2 |
b₁ = 0
| y = - | 5·x | + | 14 |
| 10 | 10 |
| y = - | x | + | 7 |
| 2 | 5 |
| m₂ = - | 1 |
| 2 |
| b₂ = | 7 |
| 5 |
m₁ = m₂ ⇒ r₁ ∥ r₂
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP01
- | Siguiente ›
Ejemplo, cómo resolver sistemas de ecuaciones lineales