Problema nº 4-a de sistemas de ecuaciones con tres incágnitas, aplicar determinantes - TP04

Enunciado del ejercicio nº 4-a

Resolver el siguiente sistema de ecuaciones con tres incógnitas:

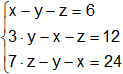
Solución

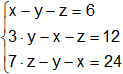
Ordenamos las ecuaciones y aplicamos determinantes:

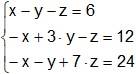
Primero calculamos el determinante del sistema:

Δ = 1·3·7 + (-1)·(-1)·(-1) + (-1)·(-1)·(-1) - [(-1)·3·(-1) + (-1)·(-1)·7 + 1·(-1)·(-1)]

Δ = 21 - 1 - 1 - (3 + 7 + 1)

Δ = 19 - 11

Δ = 8

Calculamos el determinante de "x":

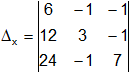
Δₓ = 6·3·7 + (-1)·24·(-1) + (-1)·12·(-1) - [(-1)·3·24 + (-1)·12·7 + 6·(-1)·(-1)]

Δₓ = 126 + 24 + 12 - (-72 - 84 + 6)

Δₓ = 162 - (-150)

Δₓ = 312

Calculamos el determinante de "y":

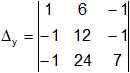
Δ_y = 1·12·7 + 6·(-1)·(-1) + (-1)·(-1)·24 - [(-1)·12·(-1) + 6·(-1)·7 + 1·(-1)·24]

Δ_y = 84 + 6 + 24 - (12 - 42 - 24)

Δ_y = 114 - (-54)

Δ_y = 168

Calculamos el determinante de "z":

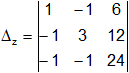
Δ_z = 1·3·24 + (-1)·(-1)·12 + 6·(-1)·(-1) - [6·3·(-1) + (-1)·(-1)·24 + 1·12·(-1)]

Δ_z = 72 + 12 + 6 - (-18 + 24 - 12)

Δ_z = 90 - (-6)

Δ_z = 96

Calculamos las incógnitas:

x = 39

y = 21

z = 12

Resultado, los valores de las incógnitas son:

x = 39

y = 21

z = 12

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP04
• | Siguiente ›

Ejemplo, cómo resolver ecuaciones con determinantes