Problema nº 4-c de sistemas de ecuaciones con tres incágnitas, por Gauss - TP04

Enunciado del ejercicio nº 4-c

Resolver el siguiente sistema de ecuaciones con tres incógnitas:

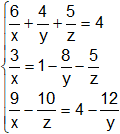
Solución

Ordenamos las ecuaciones:

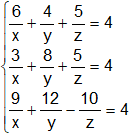
Aplicamos el método de eliminación de Gauss.

Multiplicamos la segunda ecuación por "-1" y la sumamos a la primera ecuación:

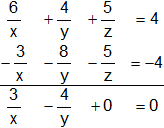
Multiplicamos la segunda ecuación por "2" y la sumamos a la tercera ecuación:

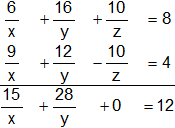
En esta primera parte el sistema queda:

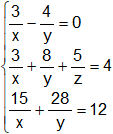
La segunda ecuación no se opera, multiplicamos la primera ecuación por "-5" y la sumamos a la tercera ecuación:

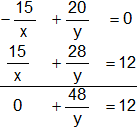
En esta segunda parte el sistema queda:

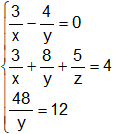
De la tercera ecuación despejamos "y" y reemplazamos en la primera ecuación:

y = 48/12

y = 4

3/x - 4/y = 0

3/x - 4/4 = 0

3/x - 1 = 0

Despejamos "x":

3/x = 1

x = 3/1

x = 3

Reemplazamos "x" e "y" en la segunda ecuación:

3/3 + 8/4 + 5/z = 4

1 + 2 + 5/z = 4

3 + 5/z = 4

5/z = 4 - 3

5/z = 1

Despejamos "z":

z = 5/1

z = 5

Resultado, los valores de las incógnitas son:

x = 3

y = 4

z = 5

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP04
• | Siguiente ›

Ejemplo, cómo resolver ecuaciones por Gauss