Problema nº 1-b de sistemas de ecuaciones con dos incágnitas, lineales - TP05
Enunciado del ejercicio nº 1-b
Resolver el siguiente sistema de ecuaciones lineales por los métodos de:
I) Igualación
II) Sustitución
III) Reducción
IV) Determinantes
V) Graficar
4·x + 3·y = 27
6·x + 3·y - 3 = 0
Solución
4·x + 3·y = 27
6·x + 3·y - 3 = 0
En la segunda ecuación sacamos factor común "3" y simplificamos:
I) Igualación
4·x + 3·y = 27
2·x + y - 1 = 0
Usaremos este sistema para todos los métodos.
Despejamos "y" en ambas ecuaciones:
| y = | -4·x + 27 |
| 3 |
y = -2·x + 1
Igualamos y resolvemos:
| -4·x + 27 | = -2·x + 1 |
| 3 |
-4·x + 27 = 3·(-2·x + 1)
-4·x + 27 = -6·x + 3
Despejamos "x":
-4·x + 6·x = -27 + 3
2·x = -24
x = -24/2
x = -12
Reemplazamos "x" en la segunda ecuación y calculamos "y":
y = -2·(-12) + 1
y = 24 + 1
y = 25
Resultado aplicando el método de igualación:
x = -12
y = 25
II) Sustitución
4·x + 3·y = 27
2·x + y - 1 = 0
Despejamos "y" de la segunda ecuación:
y = -2·x + 1
Sustituimos "y" en la primera ecuación:
4·x + 3·(-2·x + 1) = 27
Resolvemos:
4·x - 6·x + 3 = 27
-2·x = 27 - 3
-2·x = 24
Despejamos "x":
x = -24/2
x = -12
Reemplazamos "x" en la primera ecuación y calculamos "y":
| y = | -4·(-12) + 27 |
| 3 |
| y = | 48 + 27 |
| 3 |
| y = | 75 |
| 3 |
y = 25
Resultado aplicando el método de sustitución:
x = -12
y = 25
III) Reducción
4·x + 3·y = 27
2·x + y - 1 = 0
En la segunda ecuación pasamos el término independiente al otro lado del "=":
4·x + 3·y = 27
2·x + y = 1
Multiplicamos la segunda ecuación por 2 y la restamos a la primera:
4·x + 3·y = 27
2·(2·x + y) = 2·1
4·x + 3·y = 27
4·x + 2·y = 2
3·y - 2·y = 27 - 2
Despejamos "y":
y = 25
Reemplazamos "y" en la primera ecuación y calculamos "x":
4·x + 3·(25) = 27
4·x + 75 = 27
4·x = -75 + 27
4·x = -48
x = -48/4
x = -12
Resultado aplicando el método de reducción:
x = -12
y = 25
IV) Determinantes
4·x + 3·y = 27
2·x + y - 1 = 0
En la segunda ecuación pasamos el término independiente al otro lado del "=":
4·x + 3·y = 27
2·x + y = 1
| x = | Δₓ |
| Δ |
| y = | Δy |
| Δ |
Primero calculamos el determinante del sistema:
| Δ = | 4 | 3 |
| 2 | 1 |
Δ = 4·1 - 3·2
Δ = 4 - 6
Δ = -2
Hallamos los determinantes de las incógnitas:
| Δₓ = | 27 | 3 |
| 1 | 1 |
Δₓ = 27·1 - 3·1
Δₓ = 27 - 3
Δₓ = 24
| Δy = | 4 | 27 |
| 2 | 1 |
Δy = 4·1 - 27·2
Δy = 4 - 54
Δy = -50
Calculamos las incógnitas "x" e "y":
| x = | Δₓ |
| Δ |
| x = | 24 |
| -2 |
x = -12
| y = | Δy |
| Δ |
| y = | -50 |
| -2 |
y = 25
Resultado aplicando el método de determinantes:
x = -12
y = 25
Resultado, el punto de intersección es:
P(-12; 25)
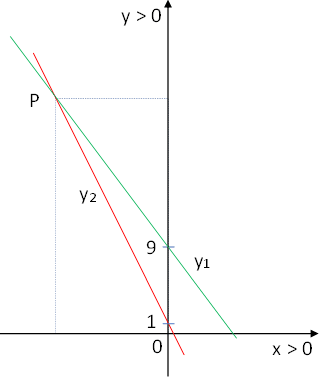
V) Gráfica
Despejamos "y" de ambas ecuaciones para obtener la ordenada al origen (b) y la pendiente (m) de las rectas:
| y = | -4·x | + | 9 |
| 3 | 1 |
| m₁ = | -4 |
| 3 |
b₁ = 9
y = -2·x + 1
| m₂ = | -2 |
| 1 |
b₂ = 1
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP05
- | Siguiente ›
Ejemplo, cómo resolver sistemas de ecuaciones lineales