Trigonometría plana
Trigonometría, rama de las matemáticas que estudia las relaciones entre los lados y los ángulos de triángulos, de las propiedades y aplicaciones de las funciones trigonométricas de ángulos. Las dos ramas fundamentales de la trigonometría son la trigonometría plana, que se ocupa de figuras contenidas en un plano, y la trigonometría esférica, que se ocupa de triángulos que forman parte de la superficie de una esfera.
Las primeras aplicaciones de la trigonometría se hicieron en los campos de la navegación, la geodesia y la astronomía, en las que el principal problema era determinar una distancia inaccesible, como la distancia entre la Tierra y la Luna, o una distancia que no podía ser medida de forma directa. Otras aplicaciones de la trigonometría se pueden encontrar en la física, química y en casi todas las ramas de la ingeniería, sobre todo en el estudio de fenómenos periódicos, como el sonido o el flujo de corriente alterna.
Trigonometría plana
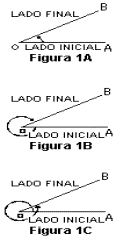
El concepto trigonométrico de ángulo es fundamental en el estudio de la trigonometría. Un ángulo trigonométrico se genera con un radio que gira. Los radios OA y OB (figuras 1a, 1b y 1c) se consideran inicialmente coincidentes con OA. El radio OB gira hasta su posición final. Un ángulo y su magnitud son positivos si se generan con un radio que gira en el sentido contrario a las agujas del reloj, y negativo si la rotación es en el sentido de las agujas del reloj. Dos ángulos trigonométricos son iguales si sus rotaciones son de igual magnitud y en la misma dirección.
Una unidad de medida angular se suele definir como la longitud del arco de circunferencia, como s en la figura 2, formado cuando los lados del ángulo central (con vértice en el centro del círculo) cortan a la circunferencia.
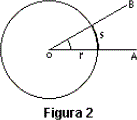
Si el arco donde s(AB) es igual a un cuarto de la circunferencia total C, es decir, s = 3·C, de manera que OA es perpendicular a OB, la unidad angular es el ángulo recto. Si s = 1·C, de manera que los tres puntos A, O y B están todos en la misma línea recta, la unidad angular es el ángulo llano. Si s = (1/360)·C, la unidad angular es un grado. Si s = Y·C, de manera que la longitud del arco es igual al radio del círculo, la unidad angular es un radián. Comparando el valor de C en las distintas unidades, se tiene que:
1 ángulo llano = 2 ángulos rectos = 180 grados = π radianes
Cada grado se subdivide en 60 partes iguales llamadas minutos, y cada minuto se divide en 60 partes iguales llamadas segundos. Si se quiere mayor exactitud, se utiliza la parte decimal de los segundos. Las medidas en radianes menores que la unidad se expresan con decimales. El símbolo de grado es °, el de minuto es ' y el de segundos es ". Las medidas en radianes se expresan o con la abreviatura rad o sin ningún símbolo. Por tanto, 61° 28' 42,14" = 1,073 rad = 1,073
Se sobreentiende que el último valor es en radianes.
Un ángulo trigonométrico se designa por convenio con la letra griega theta (θ). Si el ángulo θ está dado en radianes, entonces se puede usar la fórmula s = r·θ para calcular la longitud del arco s; si θ viene dado en grados, entonces:
s = π·r·(θ/180°)
Funciones trigonométricas
Las funciones trigonométricas son valores sin unidades que dependen de la magnitud de un ángulo. Se dice que un ángulo situado en un plano de coordenadas rectangulares está en su posición normal si su vértice coincide con el origen y su lado inicial coincide con la parte positiva del eje x.
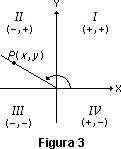
En la figura 3, el punto P está situado en una línea recta que pasa por el origen y que forma un ángulo θ con la parte positiva del eje x. Las coordenadas x e y pueden ser positivas o negativas según el cuadrante (I, II, III, IV) en que se encuentre el punto P; x será cero si el punto P está en el eje y o y será cero si P está en el eje x. La distancia r entre el punto y el origen es siempre positiva e igual a x² + y², aplicando el teorema de Pitágoras.
Las seis funciones trigonométricas más utilizadas se definen de la siguiente manera:
- Seno (sen) del ángulo θ: sen θ = y/r
- Coseno (cos) del ángulo θ: cos θ = x/r
- Tangente (tg) del ángulo θ: tg θ = y/x
- Cotangente (cotg) del ángulo θ: cotg θ = x/y
- Secante (sec) del ángulo θ: sec θ = r/x
- Cosecante (cosec) del ángulo θ: cosec θ = r/y
Como la x y la y son iguales si se añaden 2·π radianes al ángulo - es decir, si se añaden 360° - es evidente que sen (θ + 2·π) = sen θ. Lo mismo ocurre con las otras cinco funciones. Dadas sus respectivas definiciones, tres funciones son las inversas de las otras tres, es decir,
| cotg θ = | 1 |
| tg θ |
| sec θ = | 1 |
| cos θ |
| cosec θ = | 1 |
| sen θ |
Si el punto P, de la definición de función trigonométrica, se encuentra en el eje Y, la x es cero; por tanto, puesto que la división por cero no está definida en el conjunto de los números reales, la tangente y la secante de esos ángulos, como 90°, 270° y -270° no están definidas. Si el punto P está en el eje x, la y es 0; en este caso, la cotangente y la cosecante de esos ángulos, como 0°, 180° y -180° tampoco está definida. Todos los ángulos tienen seno y coseno, pues r no puede ser igual a 0.
Como r es siempre mayor o igual que la x o la y, los valores del sen θ y cos θ varían entre -1 y +1. La tg θ y la cotg θ son ilimitadas, y pueden tener cualquier valor real. La sec θ y la cosec θ pueden ser mayor o igual que +1 o menor o igual que -1.
Como se ha podido ver en los anteriores apartados, el valor de las funciones trigonométricas no depende de la longitud de r, pues las proporciones son sólo función del ángulo.
Si θ es uno de los ángulos agudos de un triángulo rectángulo (figura 4), las definiciones de las funciones trigonométricas dadas más arriba se pueden aplicar a θ como se explica a continuación. Si el vértice A estuviera situado en la intersección de los ejes X e Y de la figura 3, si AC descansara sobre la parte positiva del eje X y si B es el punto P de manera que AB = AP = r, entonces el sen θ = y/r = a/c, y así sucesivamente:
| sen θ = | Opuesto | = | a | 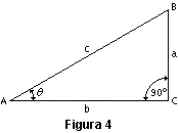 |
| Hipotenusa | c | |||
| cos θ = | Adyacente | = | b | |
| Hipotenusa | c | |||
| tg θ = | Opuesto | = | a | |
| Adyacente | b | |||
| cotg θ = | Adyacente | = | b | |
| Opuesto | a | |||
| sec θ = | Hipotenusa | = | c | |
| Adyacente | b | |||
| cosec θ = | Hipotenusa | = | c | |
| Opuesto | a | |||
Los valores numéricos de las funciones trigonométricas de ciertos ángulos se pueden obtener con facilidad. Por ejemplo, en un triángulo rectángulo isósceles, se tiene que θ = 45° y que b = a, y además se sabe, por el Teorema de Pitágoras, que c² = b² + a². De aquí se deduce que c² = 2·a² o que c = a². Por tanto
sen 45° = cos 45° = 1/√2
tg 45° = cotg 45° = 1
sec 45° = cosec 45° = √2
Los valores numéricos de las funciones trigonométricas de un ángulo cualquiera se pueden hallar de forma aproximada dibujando el ángulo en su posición normal utilizando la regla, el compás y el transportador de ángulos. Si se miden x, y y r es fácil calcular las proporciones deseadas. En realidad, basta con calcular los valores del sen θ y del cos θ para unos cuantos ángulos específicos, pues los valores de los demás ángulos y las demás funciones se calculan utilizando las igualdades que se mencionan en el siguiente apartado.
Igualdades trigonométricas
Las siguientes fórmulas, llamadas igualdades o identidades, muestran las relaciones entre las diversas funciones trigonométricas, que se cumplen para cualquier ángulo θ, o pareja de ángulos θ y φ:
I.
sen θ·cosec θ = cos θ·sec θ = tg θ·cotg θ = 1
II.
| tg θ = | sen θ | ; cotg θ = | cos θ |
| cos θ | sen θ |
III.
sen² θ + cos² θ = sec² θ - tg² θ = cosec² - cotg² θ = 1
IV.
sen (θ ± φ) = sen θ·cos φ ± cos θ·sen φ
cos (θ ± φ) = cos θ·cos φ ∓ sen θ·sen φ
| tg (θ ± φ) = | tg θ ± tg φ |
| 1 ∓ tg θ·tg φ |
V.
sen θ = -sen (-θ)
cos θ = cos (-θ)
sen θ = -sen (θ - 180°) = cos (θ - 90°)
cos θ = -cos (θ - 180°) = -sen (θ - 90°)
Utilizando con reiteración una o más fórmulas del grupo V, conocidas como fórmulas de reducción, es posible calcular el seno de θ y el coseno de θ, para cualquier valor de θ, en función del seno y del coseno de ángulos entre 0° y 90°. Utilizando las fórmulas de los grupos I y II, se pueden calcular los valores de la tangente, cotangente, secante y cosecante de θ en función del seno y del coseno. Por tanto, es suficiente tabular los valores del seno y el coseno de θ para valores de θ entre 0° y 90°. En la práctica, para evitar cálculos tediosos, se suelen también tabular las otras cuatro funciones para los mismos valores de θ. Sin embargo, desde la popularización de las calculadoras electrónicas y los ordenadores o computadoras, las tablas de funciones trigonométricas han caído en desuso.
La variación de los valores de las funciones trigonométricas para diversos ángulos se pueden representar gráficamente (ver figuras adjuntas). Se puede ver con claridad en estas curvas que todas las funciones trigonométricas son periódicas, es decir, el valor de cada una se repite a intervalos regulares llamados períodos. El período de todas las funciones, excepto la tangente y la cotangente, es 360° o 2·π radianes. La tangente y la cotangente tienen un período de 180 ° o π radianes.
Funciones inversas
La expresión "y es el seno de q", o y = sen θ, es equivalente a la expresión θ es el ángulo cuyo seno es igual a y, lo que se escribe como θ = arcsen y, o también como θ = sen⁻¹ y. Las otras funciones inversas, arccos y, arctg y, arccotg y, arcsec y, y arccosec y, se definen del mismo modo. En la expresión y = sen θ o θ = arcsen y, un valor dado de y genera un número infinito de valores de θ, puesto que sen 30° = sen 150° = sen (30° + 360°) … = 1. Por tanto, si θ = arcsen 1, entonces θ = 30° + n·360° y θ = 150° + n·360°, para cualquier entero n positivo, negativo o nulo. El valor 30° se toma como valor principal o fundamental del arcsen 1. Para todas las funciones inversas, suele darse su valor principal. Hay distintas costumbres, pero la más común es que el valor principal del arcsen y, arccos y, arctg y, arccosec y, arcsec y y arccotg y, para y positiva es un ángulo entre 0° y 90°. Si y es negativa, se utilizan los siguientes rangos:
-90° ≤ arcsen y; arctg y < 0°
90° < arccos y; arccotg y ≤ 0°
-180° ≤ arcsec y; arccosec y ≤ -90°
El triángulo general
Entre las diversas aplicaciones prácticas de la trigonometría está la de determinar distancias que no se pueden medir directamente. Estos problemas se resuelven tomando la distancia buscada como el lado de un triángulo, y midiendo los otros dos lados y los ángulos del triángulo. Una vez conocidos estos valores basta con utilizar las fórmulas que se muestran a continuación.
Si A, B y C son los tres ángulos de un triángulo y a, b, c son los tres lados opuestos respectivamente, es posible demostrar que
Las reglas del coseno y de la tangente tienen otras dos expresiones que se obtienen rotando las letras a, b, c y A, B, C.
Regla del seno
| a | = | b | = | c |
| sen A | sen B | sen C |
Regla del coseno
a² = b² + c² - 2·b·c·cos A
Regla de la tangente
| a - b | = | tg ½·(A - B) |
| a + b | tg ½·(A + B) |
Estas tres relaciones son suficientes para resolver cualquier triángulo, esto es, calcular los ángulos o lados desconocidos de un triángulo, dados: un lado y dos ángulos, dos lados y su correspondiente ángulo, dos ángulos y un ángulo opuesto a uno de ellos (que tiene dos posibles soluciones), o los tres lados.
Trigonometría esférica
La trigonometría esférica, que se usa sobre todo en navegación y astronomía, estudia triángulos esféricos, es decir, figuras formadas por arcos de circunferencias máximas contenidos en la superficie de una esfera. El triángulo esférico, al igual que el triángulo plano, tiene seis elementos, los tres lados a, b, c, y los tres ángulos A, B y C. Sin embargo, los lados de un triángulo esférico son magnitudes angulares en vez de lineales, y dado que son arcos de circunferencias máximas de una esfera, su medida viene dada por el ángulo central correspondiente. Un triángulo esférico queda definido dando tres elementos cualesquiera de los seis, pues, al igual que en la geometría plana, hay fórmulas que relacionan las distintas partes de un triángulo que se pueden utilizar para calcular los elementos desconocidos.
La trigonometría esférica es de gran importancia para la teoría de la proyección estereográfica y en la geodesia. Es también el fundamento de los cálculos astronómicos. Por ejemplo, la solución del llamado triángulo astronómico se utiliza para encontrar la latitud y longitud de un punto, la hora del día, la posición de una estrella y otras magnitudes.
Historia
La historia de la trigonometría se remonta a las primeras matemáticas conocidas, en Egipto y Babilonia. Los egipcios establecieron la medida de los ángulos en grados, minutos y segundos. Sin embargo, hasta los tiempos de la Grecia clásica no empezó a haber trigonometría en las matemáticas. En el siglo II a.C. el astrónomo Hiparco de Nicea compiló una tabla trigonométrica para resolver triángulos. Comenzando con un ángulo de 71° y yendo hasta 180 °C con incrementos de 71°, la tabla daba la longitud de la cuerda delimitada por los lados del ángulo central dado que corta a una circunferencia de radio r. Esta tabla es similar a la moderna tabla del seno. No se sabe con certeza el valor de r utilizado por Hiparco, pero sí se sabe que 300 años más tarde el astrónomo Tolomeo utilizó r = 60, pues los griegos adoptaron el sistema numérico sexagesimal (base 60) de los babilonios.
Tolomeo incorporó en su gran libro de astronomía, el Almagesto, una tabla de cuerdas con incrementos angulares de 1°, desde 0° a 180°, con un error menor que 1/3.600 de unidad. También explicó su método para compilar esta tabla de cuerdas, y a lo largo del libro dio bastantes ejemplos de cómo utilizar la tabla para calcular los elementos desconocidos de un triángulo a partir de los conocidos. Tolomeo fue el autor del que hoy se conoce como teorema de Menelao para resolver triángulos esféricos, y durante muchos siglos su trigonometría fue la introducción básica para los astrónomos. Quizás al mismo tiempo que Tolomeo los astrónomos de la India habían desarrollado también un sistema trigonométrico basado en la función seno en vez de cuerdas como los griegos. Esta función seno, al contrario que el seno utilizado en la actualidad, no era una proporción, sino la longitud del lado opuesto a un ángulo en un triángulo rectángulo de hipotenusa dada. Los matemáticos indios utilizaron diversos valores para ésta en sus tablas.
A finales del siglo VIII los astrónomos árabes habían recibido la herencia de las tradiciones de Grecia y de la India, y prefirieron trabajar con la función seno. En las últimas décadas del siglo X ya habían completado la función seno y las otras cinco funciones y habían descubierto y demostrado varios teoremas fundamentales de la trigonometría tanto para triángulos planos como esféricos. Varios matemáticos sugirieron el uso del valor r = 1 en vez de r = 60, lo que produjo los valores modernos de las funciones trigonométricas. Los árabes también incorporaron el triángulo polar en los triángulos esféricos. Todos estos descubrimientos se aplicaron a la astronomía y también se utilizaron para medir el tiempo astronómico y para encontrar la dirección de la Meca, lo que era necesario para las cinco oraciones diarias requeridas por la ley islámica. Los científicos árabes también compilaron tablas de gran exactitud. Por ejemplo, las tablas del seno y de la tangente, construidas con intervalos de 1/60 de grado (1 minuto) tenían un error menor que 1 dividido por 700 millones. Además, el gran astrónomo Nasir al-Dín al-Tusí escribió el Libro de la figura transversal, el primer estudio de las trigonometrías plana y esférica como ciencias matemáticas independientes.
El occidente latino se familiarizó con la trigonometría árabe a través de traducciones de libros de astronomía arábigos, que comenzaron a aparecer en el siglo XII. El primer trabajo importante en esta materia en Europa fue escrito por el matemático y astrónomo alemán Johann Müller, llamado Regiomontano. Durante el siguiente siglo, el también astrónomo alemán Georges Joachim, conocido como Rético, introdujo el concepto moderno de funciones trigonométricas como proporciones en vez de longitudes de ciertas líneas. El matemático francés François Viète incorporó el triángulo polar en la trigonometría esférica y encontró fórmulas para expresar las funciones de ángulos múltiples, sen n·θ y cos n·θ, en función de potencias de sen θ y cos θ.
Los cálculos trigonométricos recibieron un gran empuje gracias al matemático escocés John Napier o Neper, quien inventó los logaritmos a principios del siglo XVII. También encontró reglas mnemotécnicas para resolver triángulos esféricos, y algunas proporciones (llamadas analogías de Napier) para resolver triángulos esféricos oblicuos.
Casi exactamente medio siglo después de la publicación de los logaritmos de Napier, Isaac Newton inventó el cálculo diferencial e integral. Uno de los fundamentos del trabajo de Newton fue la representación de muchas funciones matemáticas utilizando series infinitas de potencias de la variable x. Newton encontró la serie para el sen x y series similares para el cos x y la tg x. Con la invención del cálculo las funciones trigonométricas fueron incorporadas al análisis, donde todavía hoy desempeñan un importante papel tanto en las matemáticas puras como en las aplicadas.
Por último, en el siglo XVIII, el matemático suizo Leonhard Euler definió las funciones trigonométricas utilizando expresiones con exponenciales de números complejos. Esto convirtió a la trigonometría en sólo una de las muchas aplicaciones de los números complejos; además, Euler demostró que las propiedades básicas de la trigonometría eran simplemente producto de la aritmética de los números complejos.
Aplicaciones de la unidad grado
Grado
En trigonometría, arco igual a 1/360 de la circunferencia de un círculo, o ángulo central que corresponde a dicho arco. El grado es la unidad corriente de medida de ángulos y arcos de un círculo. Se divide en 60 minutos, cada uno de los cuales equivale a 1/21.600 de la circunferencia de un círculo; cada minuto se divide en 60 segundos, cada uno de los cuales equivale a 1/1.296.000. Los grados se indican normalmente con el símbolo °, los minutos con ' y los segundos con ", como en 41° 18' 09", que se lee "41 grados 18 minutos y 9 segundos".
La medida de ángulos en grados es ampliamente usada en ingeniería y en las ciencias físicas, principalmente en astronomía, navegación y topografía. El método más corriente de localizar una estrella, o un punto en la superficie de la Tierra, es utilizar su distancia angular en grados, minutos y segundos a ciertos puntos o líneas de referencia fijadas. Los posiciones en la superficie de la Tierra se miden en grados de latitud norte o sur del ecuador y grados de longitud este u oeste del meridiano principal, que normalmente es el meridiano que pasa por Greenwich en Inglaterra.
Grados de latitud
Si la Tierra fuera una esfera exacta, un grado de latitud sería igual a 1/360 de la circunferencia de un círculo dibujado sobre la superficie de la Tierra y que pasa por los polos Norte y Sur. La Tierra, sin embargo, está achatada por los polos, por lo que la longitud de un grado, determinado astronómicamente, varía del ecuador a los polos. En el ecuador un grado de latitud son 110.568,18 m, o unos 110,57 km. La longitud de un grado a 45° N o S, llamado ángulo medio, es 111.131,9 m o alrededor de 111,13 km.
Grados de longitud
El tamaño de un grado de longitud varía desde un valor máximo en el ecuador hasta cero en los polos Norte y Sur. Esto es debido a que la longitud se mide como el arco de un paralelo de latitud dada, y los círculos que forman los paralelos disminuyen en radio al incrementar su distancia al ecuador. En el ecuador, un grado de longitud equivale a 112,09 km, pero a 40° N o S, un grado son 85,99 km. La longitud se puede medir también utilizando horas hacia el este u oeste del meridiano principal, pues una hora equivale a 15 grados y un minuto horario a 15 minutos angulares. Así, la longitud de la ciudad de México puede escribirse como 99° o como 6 horas 36 minutos al oeste de Greenwich.
Otras medidas angulares
En ciertas ramas de las matemáticas avanzadas, en particular aquéllas que incluyen cálculos, los ángulos se miden habitualmente en radianes (rad). En 360° hay 2·π rad, o unos 6,28 rad.
En el ejército, los ángulos se miden generalmente en milésimas, especialmente para la localización de objetivos de artillería. Una milésima es la medida del ángulo central formado por un arco que es 1/6.400 del círculo. Una milésima equivale a 0,05625° y, aproximadamente, 0,001 radianes.
Radián, en matemáticas, la unidad de ángulo plano igual al ángulo central formado por un arco de longitud igual al radio del círculo. La medida en radianes de un ángulo se expresa como la razón del arco formado por el ángulo, con su vértice en el centro de un círculo, y el radio de dicho círculo. Esta razón es constante para un ángulo fijo para cualquier círculo. La medida en radianes de un ángulo no es la razón de la longitud de la cuerda y el radio, sino la razón de la longitud del arco y el radio.
La medida en radianes de un ángulo y su medida en grados están relacionadas. La circunferencia de un círculo está dada por
C = 2·π·r
Donde r es el radio del círculo y π es el número 3,14159. Dado que la circunferencia de un círculo es exactamente 2·π radios, y que un arco de longitud r tiene un ángulo central de un radián, se deduce que
2·π radianes = 360 grados
Al dividir 360° por 2·π se puede ver que un radián es aproximadamente 57° 17' 44,8". En aplicaciones prácticas, las siguientes aproximaciones son lo suficientemente exactas:
Un radián = 57,3 grados
Un grado = 0,01745 radianes
El grado y el radián son unidades angulares de distinto tamaño y son intercambiables. Los ingenieros y técnicos utilizan más los grados, mientras que la medida en radianes se usa casi exclusivamente en estudios teóricos, como en el cálculo, debido a la mayor simplicidad de ciertos resultados, en especial para las derivadas y la expansión en series infinitas de las funciones trigonométricas. Como se puede ver, mientras que el símbolo ° se utiliza para indicar grados, no se utiliza ningún símbolo para indicar la medida en radianes.
Trigonometría
Grados y radianes
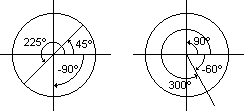
Las unidades de medida de ángulos más conocidas son los grados, minutos y segundos. Este tipo de medidas está basada en la división en partes iguales de una circunferencia.
Las equivalencias son las siguientes:
360° = un giro completo alrededor de una circunferencia.
180° = ½ vuelta alrededor de una circunferencia.
90° = ¼ de vuelta.
1° = 1/360 de vuelta, etc.
También se puede definir otra unidad angular, el radián, que en las aplicaciones físicas es mucho más practico y directo que trabajar con grados.
La magnitud de un ángulo medido en radianes está dada por la longitud del arco de circunferencia que subtiende, dividido por el valor del radio. El valor de este ángulo es independiente del valor del radio; por ejemplo, al dividir una pizza en 10 partes iguales, el ángulo de cada pedazo permanece igual, independiente si la pizza es chica, normal o familiar.
De esta forma, se puede calcular fácilmente la longitud de un arco de circunferencia; solo basta multiplicar el radio por el ángulo en radianes.
Longitud arco de circunferencia = [Ángulo en radianes]×[Radio de la circunferencia]
Ya que conocemos el perímetro de una circunferencia de radio unitario (2·π·r = 2 < Imagen >), entonces el ángulo de una circunferencia completa, medido en radianes es 2·π. Como además sabemos que este mismo ángulo, medido en grados mide 360°, entonces podemos definir una equivalencia:
1 radián = 57,29°
A partir de esta igualdad, determinamos que:
90° = π/2 radianes
60° = π/3 radianes
45° = π/4 radianes
30° = π/6 radianes
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
¿Cuál es la razón entre el cateto adyacente y la hipotenusa? ¿Cuál es la razón entre el cateto opuesto y la hipotenusa?