Trigonometría. Medidas angulares
# Recta: es una sucesión de infinitos puntos que se extiende en una misma dirección y en ambos sentidos.
![]()
# Semirrecta o Rayo: es un subconjunto de puntos de una recta. Es una recta o un segmento de recta que tiene un origen, una dirección y un sentido.
![]()
# Segmento: es una porción de una recta.
![]()
# Ángulo: es la abertura formada por la unión de 2 semirrectas en un mismo punto llamado vértice; las semirrectas reciben el nombre de lados del ángulo.
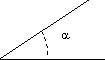
Es la figura geométrica formado por 2 rayos que tiene un punto común llamado vértice.
El ángulo se obtiene por la rotación de una semirrecta alrededor de su origen.
La posición original de la semirrecta se denomina lado inicial y la posición final se denomina lado terminal.
La rotación del ángulo se puede efectuar en 2 sentidos; en el sentido contrario a las manecillas del reloj, en éste caso el ángulo es positivo y girando en el sentido de las manecillas del reloj el ángulo es negativo.
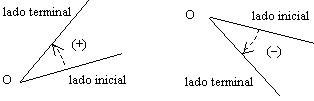
# Medición de ángulos: Medir un ángulo es compararlo con otro que se toma por unidad de medida. Para medir los ángulos existen varios sistemas, siendo los más conocidos el sistema sexagesimal y el circular.
Sistemas de medidas angulares
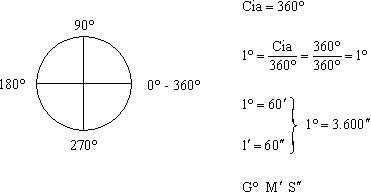
# Sistema Sexagesimal: en éste sistema la unidad de medida es el grado sexagesimal que corresponde a 1/360 que se abrevia 1°; éste a su vez se divide en 60 partes iguales y 1°/60 corresponde a un minuto sexagesimal que se abrevia 1'; éste a su vez se divide en 60 partes iguales y 1'/60 corresponde a un segundo sexagesimal que se abrevia 1".
# Sistema Circular: en éste sistema la unidad de medida es el radián.
¿Qué es el radián?: El radián es un ángulo central que tiene como lados 2 radios de una circunferencia, cuyo arco es igual al radio de la circunferencia al cual pertenece.
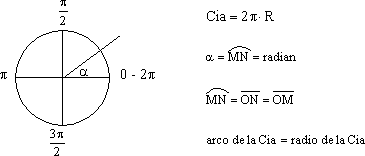
1 radián = 360°/2·π·R = 360°/6,283185307 = 57,29577951° = 57° 17' 44,8"
Siendo:
π = 3,141592654
R = 1
Las unidades de medida que pasaré a estudiar pertenecen al sistema sexagesimal y circular.
Equivalencia entre los sistemas
α°/360° = α rad/2·π
Ejercicios de aplicación
1- Expresar en grados.
| Respuesta | ||
|
a) 53° 16' 50" = b) 170° 36' 50" = c) 28° 10' = d) 45° 36" = e) 276° 09' 07" = |
53,28055556° 170,6138889° 28,16666667° 45,01° 276,1519444° |
2- Expresar en minutos.
| Respuesta | ||
|
a) 16° 29' 32" = b) 148° 19' 37" = c) 45° 10' = d) 82° 18" = |
989,5' 8.899,6' 2.710' 4.920,3' |
3- Expresar en segundos.
| Respuesta | ||
|
a) 35° 19' 43" = b) 72° 40' = c) 180° 19" = d) 342° 18' 56" = |
127.183" 261.600" 496.819" 1.232.336" |
4- Expresar en grados, minutos y segundos.
| Respuesta | ||
|
a) 38,466° = b) 126,03334° = c) 136,44' = d) 362,62' = e) 40.436" = f) 68.367" = |
38° 27' 57,6" 126° 02' 2° 16' 26,4" 6° 02' 37,2" 11° 13' 56" 18° 59' 27" |
5- Reducir al sistema circular. Para π = 3,14.
| Respuesta | ||
|
a) 42° 29' 36" = b) 150° = c) 36° 18' = d) 146° 36" = e) 184,68' = f) 58.348" = g) 270° = |
0,74 rad 2,61 rad = ⅚·π rad 0,63 rad 2,54 rad 0,05 rad 0,28 rad 4,71 rad = (3/2)·π rad |
6- Reducir al sistema sexagesimal.
| Respuesta | ||
|
a) 1,36 rad = b) 0,28 rad = c) (3/2)·π rad = d) ¾·π rad = e) ⅖·π rad = f) (3/7)·π rad = g) (5/9)·π rad = h) (11/12)·π rad = |
77° 57' 42,42" 16° 03' 03,44" 270° 42° 59' 37,07" 72° 77° 08' 34,29" 100° 165° |
Ejercicios de aplicación
Se considera para π = 3,14.
1- Expresar en el sistema circular un ángulo de:
| Respuesta | ||
|
a) 18° = b) 30° = c) 36° = d) 43° = e) 45° = f) 60° = g) 72° = h) 75° = i) 80° = j) 120° = k) 161° = l) 540° = m) 35° 40' = n) 42° 27' 32" = o) 42° 59' 37" = p) 46° 20' 30" = q) 55° 84' = r) 97° 25' = s) 150° 03' 24" = |
(⅒)·π rad ⅙·π rad (⅕)·π rad 0,75 rad ¼·π rad ⅓·π rad ⅖·π rad (5/12)·π rad (4/9)·π rad ⅔·π rad 2,81 rad 3·π rad 0,62 rad 0,74 rad 0,75 rad 0,81 rad 0,98 rad 1,70 rad 2,61 rad |
2- Expresar en el sistema sexagesimal un ángulo de:
| Respuesta | ||
|
a) (1/12)·π rad = b) ⅛·π rad = c) (⅕)·π rad = d) 1 rad = e) ⅗·π rad = f) ⅔·π rad = g) ¾·π rad = h) 2,5 rad = i) ⅘·π rad = j) 2,7 rad = k) 3,6 rad = l) (4/3)·π rad = m) 4,18888 rad = n) (7/5)·π rad = o) (5/3)·π rad = p) (7/4)·π rad = q) 5,55555 rad = r) 6 rad = s) 6,17222 rad = t) (7/3)·π rad = |
15° 22° 30' 36° 57° 19' 29,43" 108° 120° 135° 143° 18' 43,5" 144° 154° 46' 37,4" 206° 22' 09,94" 240° 240° 07' 36,76" 252° 300° 315° 318° 28' 15,6" 343° 56' 56,5" 353° 49' 17,5" 420° |
Autor: Hugo David Giménez Ayala. Paraguay.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).